Giải bài tập trang 118, 119 bài 4 Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c) Sách giáo khoa (SGK) Toán 7. Câu 24: Vẽ tam giác ABC biết…
Bài 24 trang 118 – Sách giáo khoa toán 7 tập 1
Vẽ tam giác ABC biết (widehat{A})= 900 AB=AC=3cm. Sau đó đo các góc B và C.
Giải:
Bạn đang xem: Giải bài 24, 25, 26, 27, 28 trang 118, 119 SGK Toán 7
Cách vẽ:
– Vẽ góc (widehat{xAy})=900
– Trên tia Ax vẽ đoạn thẳng AB= 3cm,
– Trên tia Ay vẽ đoạn thẳng AC= 3cm,
– Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các góc B và C ta được (widehat{B})= (widehat{C})=450
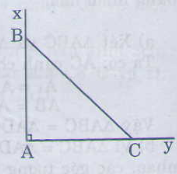
Bài 25 trang 118 – Sách giáo khoa toán 7 tập 1
Trên mỗi hình sau có các tam giác nào bằng nhau? Vì sao?

Giải:
Hình 82.
Xét (∆ADB) và (∆ADE) có:
+) (AB=AE) (gt)
+) (widehat{A_{1}}=widehat{A_{2}}),
+) (AD) chung.
Nên (∆ADB = ∆ADE(c.g.c))
Hình 83.
Xét (∆HGK) và (∆IKG) có:
+) (HG=IK) (gt)
+) (widehat{G})=(widehat{K})(gt)
+) (GK) là cạnh chung
Suy ra (∆HGK = ∆IKG( c.g.c))
Hình 84.
(∆PMQ) và (∆PMN) có:
(MP) cạnh chung
(widehat{M_{1}})=(widehat{M_{2}})
Nhưng (MN) không bằng (MQ). Nên (PMQ) không bằng (PMN).
Bài 26 trang 118 – Sách giáo khoa toán 7 tập 1
Xét bài toán:
” Cho tam giác ABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm E sao cho ME=MA. Chứng minh rẳng AB//CE’.
Dưới đây là hình vẽ và giả thiết, kết luận của bài toán(h.85)


Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:
1) MB = MC(gt)
(widehat{AMB})=(widehat{EMC}) (Hai góc đối đỉnh)
MA= ME(Giả thiết)
2) Do đó ∆AMB=∆EMC(c.g.c)
3) (widehat{MAB})=(widehat{MEC})=> AB//CE(hai góc bằng nhau ở vị trí sole trong)
4) ∆AMB= ∆EMC => (widehat{MAB})=(widehat{MEC}) (Hai góc tương ứng)
5) ∆AMB và ∆EMC có:
Giải:
Thứ tự sắp xếp là: 5,1,2,4,3
Bài 27 trang 119 – Sách giáo khoa toán 7 tập 1
Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh-góc- cạnh.
a) (∆ABC= ∆ADC) (h.86);
b) (∆AMB= ∆EMC) (H.87)
c) (∆CAB= ∆DBA). (h.88)

Giải:
a) Bổ sung thêm (widehat{BAC})=(widehat{DAC}).
b) Bổ sung thêm (MA=ME)
c) Bổ sung thêm (AC=BD)
Bài 28 trang 120 – Sách giáo khoa toán 7 tập 1
Trên hình 89 có bao nhiêu tam giác bằng nhau.

Giải:
Tam giác (DKE) có:
(widehat{D}+widehat{K}+widehat{E}=180^0) (tổng ba góc trong của tam giác).
(widehat{D}+80^0 +40^0=180^0)
(widehat{D}=180^0-120^0=60^0)
Xét (∆ ABC) và (∆KDE) có:
+) (AB=KD) (gt)
+) (widehat{B}=widehat{D}=60^0)
+) (BC= ED) (gt)
Do đó (∆ABC= ∆KDE(c.g.c))
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp



