Các dạng toán về căn bậc 2, căn bậc 3 và cách giải. Căn bậc 2 và căn bậc 3 là bài đầu tiên trong chương trình đại số toán lớp 9, đây là nội dung quan trọng vì các dạng toán về căn bậc hai và căn bậc ba thường xuất hiện trong các đề thi tuyển sinh vào lớp 10.
Để giải các dạng bài tập về căn bậc 2, căn bậc 3 thì các em cần nắm vững phần nội dung lý thuyết cùng các dạng bài tập về căn bậc 2 và bậc 3. Bài viết dưới đây sẽ hệ thống lại các dạng toán về căn bậc 2 và căn bậc 3 thường gặp để các em có thể nắm vững nội dung này.
A. Kiến thức cần nhớ về căn bậc 2 căn bậc 3
I. Căn bậc 2
1. Căn bậc 2 là gì?
– Định nghĩa: Căn bậc hai của 1 số không âm a là số x sao cho x2 = a.
– Số dương a có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là 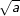 , số âm kí hiệu là
, số âm kí hiệu là 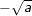 .
.
– Số 0 có đúng một căn bậc hai là chính số 0, ta viết 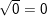
– Với số dương a, số 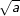 là căn bậc hai số học của a. Số 0 cũng là căn bậc hai số học của 0.
là căn bậc hai số học của a. Số 0 cũng là căn bậc hai số học của 0.
2. Tính chất của căn thức bậc 2
a) 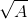 có nghĩa khi A ≥0.
có nghĩa khi A ≥0.
b) ![]()
c) 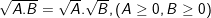
d) ![]()
3. Các phép biến đổi căn thức bậc 2 cơ bản
a) 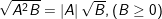
• 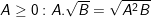
• 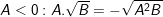
b) ![]()
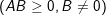
c) ![]()
d) ![]()
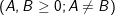
e) 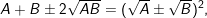
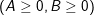
f) 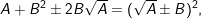
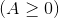
II. Căn bậc 3
1. Căn bậc là gì?
– Định nghĩa: Căn bậc ba của một số a là số x sao cho x3 = a.
2. Tính chất của căn bậc 3
– Mọi số a đề có duy nhất một căn bậc 3.
• ![small A< BLeftrightarrow sqrt[3]{A}< sqrt[3]{B}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243463656y3b4bhqyp_1624354651.gif)
• ![small sqrt[3]{A.B}=sqrt[3]{A}.sqrt[3]{B}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346366cbaaz7w1xf_1624354652.gif)
• ![]()

B. Các dạng toán về căn bậc 2 căn bậc 3
• Dạng 1: Tìm điều kiện của biến để biểu thức có nghĩa
* Phương pháp
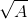 có nghĩa khi A ≥0.
có nghĩa khi A ≥0.
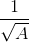 có nghĩa khi A>0
có nghĩa khi A>0
– Giải bất phương trình để tìm giá trị của biến
Ví dụ: Tìm giá trị của x để biểu thức sau có nghĩa
1. 
* Hướng dẫn:  có nghĩa khi (5-2x)≥0
có nghĩa khi (5-2x)≥0
⇔ 5 ≥ 2x ⇔ x ≤ 
2. 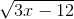
* Hướng dẫn: 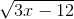 có nghĩa khi (3x-12)≥0
có nghĩa khi (3x-12)≥0
⇔ 3x ≥ 12 ⇔ x ≥ 4
3. ![]()
* Hướng dẫn: ![]() có nghĩa khi x2 > 0 ⇔ x > 0
có nghĩa khi x2 > 0 ⇔ x > 0
4. ![]()
* Hướng dẫn: căn thức có nghĩa khi ![]()
⇔ 3x – 6 < 0 ⇔ x < 2
• Dạng 2: Rút gọn biểu thức chứa căn thức
* Phương pháp
– Vận dụng hằng đẳng thức để rút gọn: ![]()
Ví dụ: Rút gọn các biểu thức sau
1. ![]()
* Hướng dẫn:
– Ta có: ![]()
vì 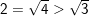
2. ![]()
* Hướng dẫn:
– Ta có: ![]()
– Vì 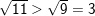
• Dạng 3: Thực hiện phép tính rút gọn biểu thức
* Phương pháp
– Vận dụng các phép biến đổi và đặt nhân tử chung
Ví dụ: Rút gọn các biểu thức sau
1. 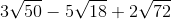
* Hướng dẫn:
– Ta có: 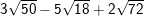
= 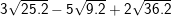
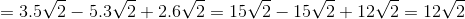
2. ![]()
* Hướng dẫn:
– Ta có: ![]()
![]()
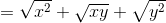
• Dạng 4: Giải phương trình có chứa căn thức
+ Dạng: 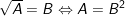 (nếu B>0).
(nếu B>0).
+ Dạng: ![]() (nếu B là một biểu thức chứa biến)
(nếu B là một biểu thức chứa biến)
+ Dạng: ![]()
+ Dạng: 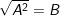 , ta đưa về dạng phương trình chứa dấu giá trị tuyệt đối:
, ta đưa về dạng phương trình chứa dấu giá trị tuyệt đối: 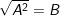
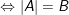
° Trường hợp 1: Nếu B là một số dương thì: ![]()
° Trường hợp 2: Nế B là một biểu thức chứa biến thì: ![]()
Ví dụ: Giải phương trình sau
1. 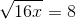
* Hướng dẫn: Để căn thức có nghĩa khi x ≥ 0
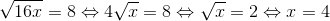
– Kết luận: x=4 là nghiệm
2. 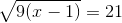
* Hướng dẫn: Để căn thức có nghĩa khi x ≥ 1, ta có
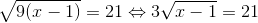
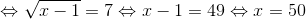
• Dạng 5: Chứng minh các đẳng thức
* Phương pháp:
– Thực hiện các phép biến đổi đẳng thức chứa căn bậc 2
– Vận dụng phương pháp chứng minh đẳng thức A = B
+ Chứng minh A = C và B = C
+ Biến đổi A về B hoặc B về A (tức A = B)
* Ví dụ: Chứng minh đẳng thức
1. 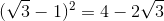
* Hướng dẫn:
– Ta có: 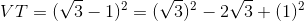
= 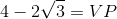
– Vậy ta có điều cần chứng minh
2. ![]()
* Hướng dẫn:
– Ta có: ![]()
![]()
– Thay vào vết trái ta có:
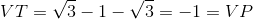
– Ta được điều cần chứng minh.
C. Bài tập về Căn bậc 2, Căn bậc 3
* Bài 2 (trang 6 SGK Toán 9 Tập 1): So sánh:
a) 2 và √3; b) 6 và √41; c) 7 và √47
* Lời giải bài 2 trang 6 SGK Toán 9 Tập 1:
a) Ta có: 2 = √4 mà 4 > 3 ⇒ √4 > √3 (Định lý)
– Kết luận: 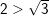
b) Ta có: 6 = √36 mà 36 < 41 ⇒ √36 < √41
– Kết luận: 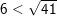
c) Ta có: 7 = √49 mà 49 > 47 ⇒ √49 > √47
– Kết luận: 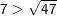
* Bài 4 (trang 7 SGK Toán 9 Tập 1): Tìm số x không âm, biết:
a) 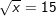 b)
b) 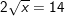
c) 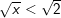 d)
d) 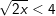
* Lời giải bài 4 trang 7 SGK Toán 9 Tập 1:
– Lưu ý: Vì x không âm (tức là x ≥ 0) nên các căn thức trong bài đều xác định.
a) 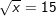
– Vì x ≥ 0 nên bình phương hai vế ta được: x = 152 ⇔ x = 225
– Kết luận: x = 225
b) 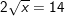 ⇔
⇔ 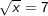
– Vì x ≥ 0 nên bình phương hai vế ta được: x = 72 ⇔ x = 49
– Kết luận: x = 49
c) 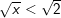
– Vì x ≥ 0 nên bình phương hai vế ta được: x < 2
– Kết luận: 0 ≤ x < 2
d) 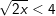
– Vì x ≥ 0 nên bình phương hai vế ta được: 2x < 16 ⇔ x < 8
– Kết luận: 0 ≤ x < 8
* Bài 6 (trang 10 SGK Toán 9 Tập 1): Với giá trị nào của a thì mỗi căn thức sau có nghĩa:
a)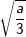 b)
b)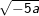 c)
c)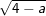 d)
d)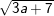
* Lời giải bài 6 trang 10 SGK Toán 9 Tập 1:
a) Điều kiện xác định cả 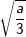 là
là 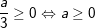
b) Tương tự: -5a ≥ 0 ⇔ a ≤ 0
c) Tương tự: 4 – a ≥ 0 ⇔ -a ≥ -4 = > a ≤ 4
d) Tương tự: 3a + 7 ≥ 0 ⇔ 3a ≥ -7 ⇔ a ≥ -7/3.
* Bài 7 (trang 10 SGK Toán 9 Tập 1): Tính:
a)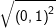 b)
b)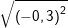 c)
c)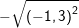 d)
d)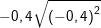
* Lời giải bài 7 trang 10 SGK Toán 9 Tập 1:
a) Ta có: 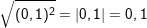
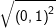
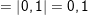
b) Ta có: 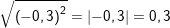
c) Ta có: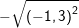
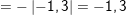
d) Ta có: 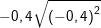
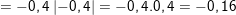
* Bài 8 (trang 10 SGK Toán 9 Tập 1): Rút gọn các biểu thức sau:
a)![]() b)
b)![]()
c) 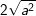 với a≥0. d)
với a≥0. d)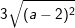 với a<2.
với a<2.
* Lời giải bài 8 trang 10 SGK Toán 9 Tập 1:
a)![]()
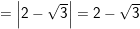 (vì
(vì 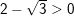 do
do 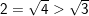 )
)
b) ![]()
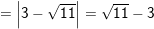 (vì √11 – 3 > 0 do 3 = √9 mà √11 > √9)
(vì √11 – 3 > 0 do 3 = √9 mà √11 > √9)
c) 2√a2 = 2|a| = 2a với a ≥ 0
d) 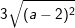
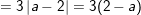 (vì a < 2 nên 2 – a > 0)
(vì a < 2 nên 2 – a > 0)
* Bài 9 (trang 11 SGK Toán 9 Tập 1): Tìm x biết:
a)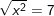 b)
b)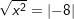 c)
c)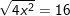 d)
d)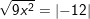
* Lời giải bài 9 trang 11 SGK Toán 9 Tập 1:
a) 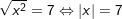
![]()
b) 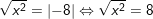
![]()
c) 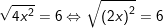
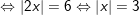
![]()
d) 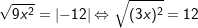
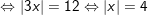
![]()
* Bài 10 (trang 11 SGK Toán 9 Tập 1): Chứng minh:
a)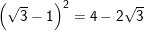
b)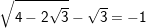
* Lời giải bài 10 trang 11 SGK Toán 9 Tập 1:
a) Ta có: VT = (√3 – 1)2 = (√3)2 – 2√3 + 1 = 3 – 2√3 + 1 = 4 – 2√3 = VP
⇒ (√3 – 1)2 = 4 – 2√3 (đpcm)
b) Ta có: 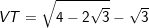
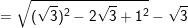
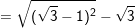
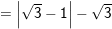
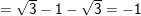 = VP (đpcm).
= VP (đpcm).
* Bài 14 (trang 11 SGK Toán 9 Tập 1): Phân tích thành nhân tử:
a) x2 – 3. b) x2 – 6 c) x2 + 2√3 x + 3. d) x2 – 2√5 x + 5
* Lời giải bài 14 trang 11 SGK Toán 9 Tập 1:
a) x2 – 3 = x2 – (√3)2 = (x – √3)(x + √3)
b) x2 – 6 = x2 – (√6)2 = (x – √6)(x + √6)
c) x2 + 2√3.x + 3 = x2 + 2√3.x + (√3)2 = (x + √3)2
d) x2 – 2√5.x + 5 = x2 – 2√5.x + (√5)2 = (x – √5)2
* Bài 67 (trang 36 SGK Toán 9 Tập 1): Hãy tìm ![small sqrt[3]{512}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243463969i5r645p97_1624354682.gif) ;
; ![small sqrt[3]{-729}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346396zj3bjf8r96_1624354682.gif) ;
; ![small sqrt[3]{0,064}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346396gs2ncubkac_1624354682.gif) ;
; ![small sqrt[3]{-0,216}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346396zmyu2l1jqm_1624354683.gif) ;
; ![small sqrt[3]{-0,008}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/162434639795359skiau_1624354683.gif)
* Lời giải bài 67 trang 36 SGK Toán 9 Tập 1:
– Ta có: ![small dpi{100} fn_cm small sqrt[3]{512}=sqrt[3]{8^{3}}=8](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346397gj7ai75vzu_1624354683.gif)
– Ta có: ![small dpi{100} fn_cm small sqrt[3]{-729}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243463973dg96twbtd_1624354683.gif)
![small =sqrt[3]{(-9)^{3}}=-9](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346397efay8l3ltn_1624354684.gif)
– Ta có: ![small dpi{100} fn_cm small sqrt[3]{0,064}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346398a1x6y62tq8_1624354684.gif)
![small =sqrt[3]{left (0,4 ight )^{3}}=0,4](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346398cadefw483n_1624354684.gif)
– Ta có: ![small dpi{100} fn_cm small sqrt[3]{-0,216}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346398mu797bn9ma_1624354684.gif)
![small =sqrt[3]{left (-0,6 ight )^{3}}=-0,6](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346398m5q7g60041_1624354685.gif)
– Ta có: ![small dpi{100} fn_cm small sqrt[3]{-0,008}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346399t4d53hndts_1624354685.gif)
![small =sqrt[3]{(-0,2)^{3}}=-0,2](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346399myac91427n_1624354685.gif)
* Lưu ý: Bạn có thể tìm các căn bậc ba ở trên bằng máy tính bỏ túi và ghi nhớ một số lũy thừa bậc 3 của các số < 10: 23 = 8; 33 = 27; 43 = 64; 53 = 125; 63 = 216; 73 = 343; 83 = 512; 93 = 729;
* Bài 68 (trang 36 SGK Toán 9 Tập 1): Tính
a) ![small sqrt[3]{27}-sqrt[3]{-8}-sqrt[3]{125}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346399na7d2lfwf9_1624354686.gif)
b) ![]()
* Lời giải bài 68 trang 36 SGK Toán 9 Tập 1:
a) ![small sqrt[3]{27}-sqrt[3]{-8}-sqrt[3]{125}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346399na7d2lfwf9_1624354686.gif)
![small =sqrt[3]{3^{3}}-sqrt[3]{(-2)^{3}}-sqrt[3]{5^{3}}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346400pbbjzr4cio_1624354686.gif)
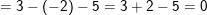
b) ![]()
![]()
![small = sqrt[3]{27}-sqrt[3]{216}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243464011lkgn4lm52_1624354687.gif)
![small =sqrt[3]{3^{3}}-sqrt[3]{6^{3}}=3-6=-3](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243464019tj3i0vwgt_1624354688.gif)
* Bài 69 (trang 36 SGK Toán 9 Tập 1): So sánh
a) 5 và ∛123. b) 5∛6 và 6∛5.
* Lời giải bài 69 trang 36 SGK Toán 9 Tập 1:
a) Ta có:![small 5=sqrt[3]5^{3}{}=sqrt[3]{125}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/16243464028kncoks51v_1624354688.gif) >
> ![small sqrt[3]{123}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346402ozfxrx9xeu_1624354688.gif) ⇒
⇒ ![small 5> sqrt[3]{123}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346402smz0dhw4or_1624354689.gif)
b) Ta có: ![small dpi{100} fn_cm small 5sqrt[3]{6}=sqrt[3]{5^{3}.6}=sqrt[3]{125.6}=sqrt[3]{750}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346402mo19f9uneg_1624354689.gif) ;
; ![small 6sqrt[3]{5}=sqrt[3]{6^{3}.5}=sqrt[3]{216.5}=sqrt[3]{1080}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346403fkxj389a24_1624354689.gif)
– Vì ![small sqrt[3]{750}< sqrt[3]{1080}](https://hayhochoi.vn/uploads/news/wyswyg/2021_06/1624346403o8s73f4qi9_1624354689.gif) ⇒ 5∛6 < 6∛5
⇒ 5∛6 < 6∛5
D. Bài tập luyện tập căn bậc 2 căn bậc 3
Bài tập 1: Với giá trị nào của x thì mỗi căn thức sau có nghĩa
a) 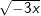 b)
b) 
c) 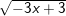 d)
d) 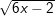
Bài tập 2: Với giá trị nào của x thì mỗi căn thức sau có nghĩa
a) ![]() b)
b) ![]() c)
c) ![]()
Bài tập 3: Với giá trị nào của x thì mỗi căn thức sau có nghĩa
a) 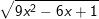 b)
b) 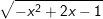
c) 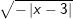 d)
d) 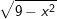
e) 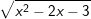 f)
f) 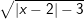
g) ![]() h)
h) ![]()
Bài tập 4: Thực hiện các phép tính sau
a) 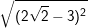 b)
b) ![]()
c) 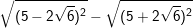
d) 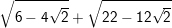
Bài tập 5: Rút gọn các biểu thức sau
a) 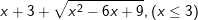
b) 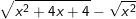 ,
, 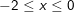
c) ![]()
d) ![]()
Bài tập 6: Giải các phương trình sau
a) 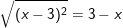
b) 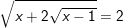
c) 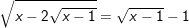
d) 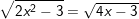
e) 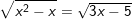
f) 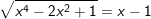
g) 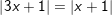
h) 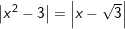
i) 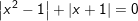
k) 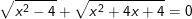
* Đáp số: a) x≤3; b) x=2; c) x≥2; d) x=2; e) vô nghiệm;
f) x=1; g) x=0; x=-1/2; h) x=√3; x=-1-√3; i) x=-1; k) x-2;
Hy vọng với bài viết về các dạng toán căn bậc 2 căn bậc 3 và bài tập vận dụng ở trên hữu ích với các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để thầy cô trường THPT Thành phố Sóc Trăng ghi nhận và hỗ trợ, chúc các em học tập tốt.
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





