Định lí Miquel, các tính chất liên quan và một số bài tập áp dụng
Bài viết hôm nay, sẽ giới thiệu đến quý bạn đọc định lí Miquel, tính chất liên quan và một số bài tập áp dụng. Hãy dành thời gian chia sẻ để nắm chắc hơn về chuyên đề này để áp dụng giải một số bài toán liên quan cực nhanh bạn nhé !
I. ĐỊNH LÍ MIQUEL LÀ GÌ ?
Định lí Miquel là định lí được đặt theo tên Auguste Mique nói về ba đường tròn mỗi đường tròn đi qua 2 điểm trên hai cạnh của tam giác và một đỉnh chung của hai cạnh đó.
Bạn đang xem: Định lí Miquel, các tính chất liên quan và một số bài tập áp dụng
Định lí:
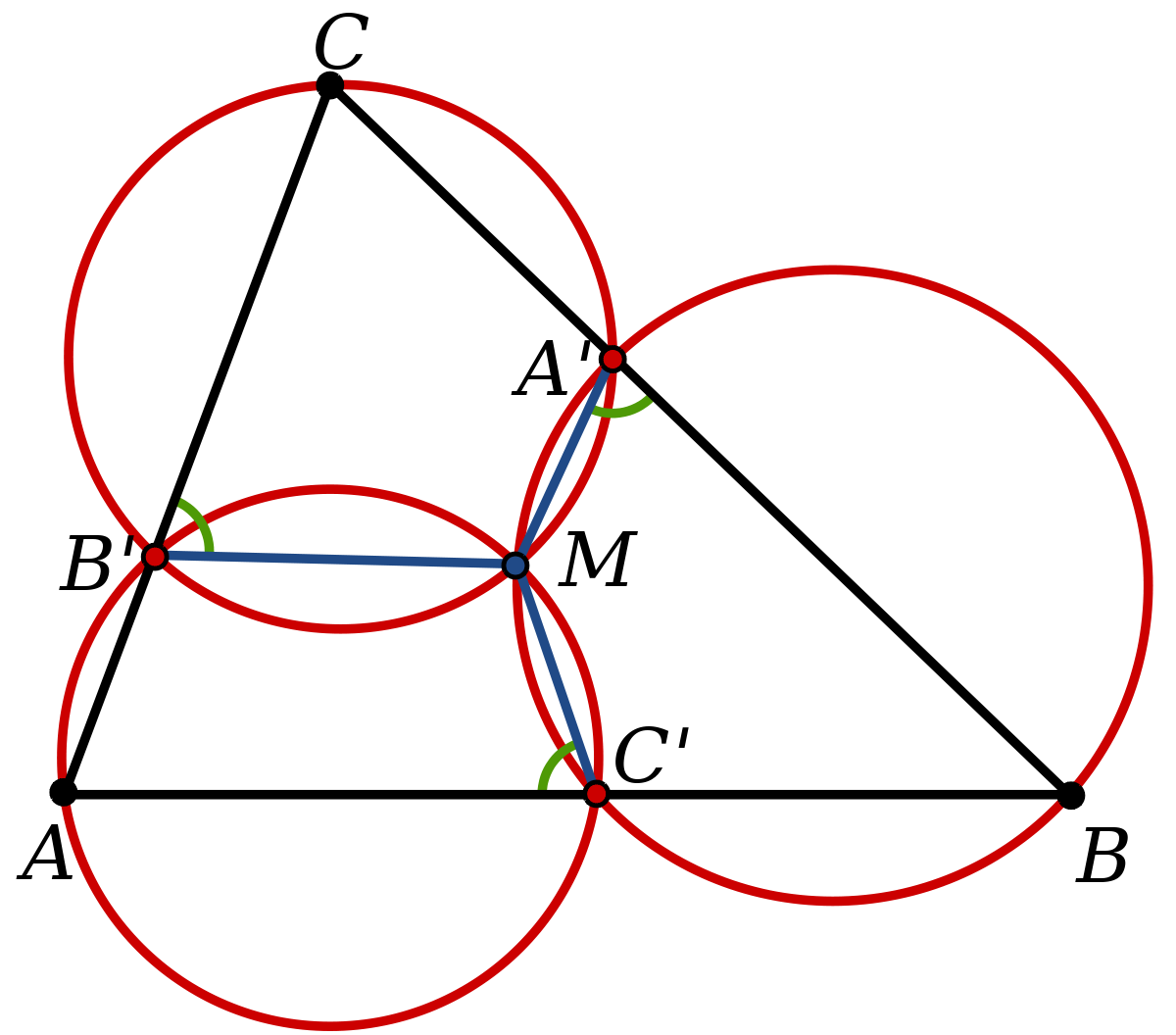
Cho tam giác ABC, với các điểm A´, B´ và C´ lần lượt trên các cạnh BC, AC, và AB khi đó đường tròn ngoại tiếp các tam giác AB´C´, A´BC´, và A´BC’ sẽ đồng quy tại điểm M gọi là điểm Miquel
– Nếu A’, B’,C’ lần lượt là trung điểm các cạnh BC, AC và AB thì điểm Miquel là tâm đường tròn ngoại tiếp tam giác ABC
– Nếu A’, B’, C’ là lần lượt là chân hình chiếu của A, B, C trên BC, AC , AB thì điểm Miquel là trực tâm của tam giác ABC
II. TÍNH CHẤT CỦA ĐỊNH LÍ MIQUEL
Định lí Miquel có các tính chất sau:
Tính chất 1. Cho tứ giác toàn phần ABCDEF. Khi đó đường tròn ngoại tiếp các tam giác ABF, DCF, BCE, ADE đồng quy.
Tính chất 2. Tâm của các đường tròn ngoại tiếp các tam giác CBE, CDF, ADE, ABF và điểm Miquel M cùng thuộc một đường tròn. Đường tròn này được gọi là đường tròn Miquel của tứ giác toàn phần.
Tính chất 3. Chân các đường vuông góc hạ từ điểm Miquel M lên các đường thẳng AB, BC, CD, DA cùng nằm trên một đường thẳng – đường thẳng Simson.
Tính chất 4. Điểm Miquel M là tâm vị tự quay của tứ giác ABCD, nghĩa là tồn tại các phép vị tự quay tâm M biến AB thành CD, AD thành BC.
Tính chất 5 (Định lí Emelyanov). Gọi X = AC ∩ BD,Y = BD ∩ EF, Z = EF ∩ AC. M là điểm Miquel của tứ giác toàn phần ABCDEF. Khi đó M nằm trên đường tròn Euler của tam giác XYZ.
Tính chất 6 (Định lí Mannheim). Cho tam giác ABC. Gọi D, E, F lần lượt là các điểm nằm trên BC, CA, AB không trùng với A, B, C.M là điểm Miquel của D, E, F ứng với tam giác ABC.P, Q, R lần lượt là các điểm nằm trên đường tròn ngoại tiếp các tam giác DEF, BFD, CDE ( các điểm P.Q.R không trùng với M).
Khi đó:
a. M, P, Q, R thẳng hàng khi và chỉ khi AP, BQ, CR đôi một song song.
b. M, P, Q, R đồng viên khi và chỉ khi AP, BQ, CR đồng quy
Tính chất 7. Cho tam giác ABC nội tiếp đường tròn (O). H là một điểm bất kì trong tam giác. Một đường thẳng bất kì qua H cắt AC, BA lần lượt tại M, N. Trên BC lấy các điểm P, Q sao cho MP k BH, NQ k CH. NQ cắt MP tại R.NQ cắt AC tại X. Chứng minh rằng NXCBAQ, CQRMPX có chung điểm Miquel.
Tính chất 8. Cho tứ giác toàn phần ABCDEF. M là điểm Miquel của tứ giác toàn phần. Các tiếp tuyến tại M của các đường tròn (FAB),(EBC),(DCF),(EAD) theo thứ tự cắt các đường thẳng AB, BC, CD, DA tại X,Y, Z, W.
a. Hai đường tròn (FWY),(EXZ) tiếp xúc với nhau tại M.
b. Trong trường hợp tứ giác ABCD không nội tiếp, thì X,Y, Z, W đồng viên.
c. Trong trường hợp tứ giác ABCD nội tiếp, thì X,Y, Z, W thẳng hàng.
III. ỨNG DỤNG ĐỊNH LÍ MIQUEL GIẢI BÀI TẬP
1. Bài tập có lời giải
Bài 1: Cho tam giác ABC. Gọi P.Q là các điểm bất kì trên cạnh BC sao cho BP = CQ và P nằm giữa B, Q. Đường tròn ngoại tiếp tam giác APQ cắt các đoạn AB, AC lần lượt tại E, F.EP, FQ cắt nhau tại T. Hai đường thẳng đi qua trung điểm của BC và song song với AB, AC lần lượt cắt EP, FQ tại X,Y. Chứng Minh rằng đường tròn ngoại tiếp tam giác TXY tiếp xúc với đường tròn ngoại tiếp tam giác APQ.
Lời giải: Gọi M là trung điểm của đoạn BC, S là giao điểm thứ hai của đường thẳng AM với đường tròn ngoại tiếp tam giác APQ.
Do MX // AB nên Góc MXP =góc MXE = góc BEP= góc PSA = góc PSM Suy ra tứ giác MSXP nội tiếp. Do đó S thuộc đường tròn ngoại tiếp tam giác PMX. Tương tự do MY // AC nên Góc MYQ = góc MYF = góc QFC = góc ASQ = góc MSQ
Suy ra tứ giác MSYQ nội tiếp. Do đó S thuộc đường tròn ngoại tiếp tam giác QMY. Từ đây suy ra S thuộc cả hai đường tròn ngoại tiếp các tam giác PMX, QMY, nên theo định lí Miquel thì S thuộc đường tròn ngoại tiếp tam giác TXY.
Do MX k BE, MY k FC, nên suy ra MX/BE =MP/BP =MQ/CQ =MY/FC ⇒MX/MY =BE/CF (1) và BE.BA = BP.BQ = CQ.CP = CF.CA ⇒ BE/CF =AC/AB. (2)
Từ (1) và (2) suy ra MX/MY =AC/AB.
Lại có Góc XMY = góc XMS + góc SMY = góc BAS + góc CAS = góc A.
Do đó ∆ABC ∼ ∆MYX(c.g.c) ⇒ góc ACB = góc QMY = góc QSY =góc MXY = MXS + SXY
= QPS + SXY
⇒ góc QSY = góc QPS + SXY
Từ đây suy ra đường tròn ngoại tiếp tam giác TXY tiếp xúc với đường tròn ngoại tiếp tam giác APQ.
Bài 2: Cho tam giác ABC có điểm D di chuyển trên cạnh BC. Dựng E, F lần lượt trên AC và AB sao cho BF = CD, CE = BD. P à giao điểm thứ hai của hai đường tròn ngoại tiếp các tam giác BDF, CDE. Chứng minh rằng tồn tại điểm Q cố định sao cho độ dài PQ là hằng số.
Lời giải. Gọi I là tâm đường tròn nội tiếp tam giác ABC. G là điểm trên BC sao cho CG = BD.
Nhận thấy: G, E đối xứng với nhau qua IC suy ra IE = IG = IF. Tam giác AEF có I là giao phân giác góc EAF [ và trung trực đoạn EF. Vậy I nằm trên đường tròn ngoại tiếp tam giác AEF.
Theo định lí Miquel ta có đường tròn ngoại tiếp tam giác AEF đi qua điểm P. Gọi Y là giao điểm thứ hai của đường thẳng BI với đường tròn ngoại tiếp tam giác BDF, Z là giao điểm thứ hai của đường thẳng C I với đường tròn ngoại tiếp tam giác CDE.
Ta có
YF = YD, FB = DC, góc YFB = góc YDC
Suy ra ∆YFB = ∆YDC ⇒ YB = YC. Chứng minh tương tự ta có ZB = ZC . Vậy Y, Z là giao của trung trực đoạn BC với IB, IC. Suy ra Y, Z cố định. Áp dụng tính chất 6 ta có I,Y, Z, P đồng viên. Vậy P nằm trên đường tròn ngoại tiếp tam giác IYZ cố định. Gọi Q là tâm của đường tròn này, ta có PQ cố định, không phụ thuôc vào vị trí của D.
Bài 3:Cho tứ giác ABCD nội tiếp đường tròn (O) và ABCD không phải là hình thang. Gọi E là giao điểm của AC và BD, P là một điểm
thuộc đường thẳng OE. Đường tròn ngoại tiếp tam giác PAD và PBC cắt nhau tại điểm thứ hai Q.
a. Chứng minh rằng Q thuộc một đường tròn cố định khi P di chuyển.
b. Đường tròn ngoại tiếp tam giác PAB, PCD cắt nhau tại điểm thứ hai R. Chứng minh
rằng đường thẳng QR luôn đi qua một điểm cố định khi P di chuyển.
Lời giải.
a. Gọi M là giao điểm của AD và BC, N là giao điểm của AB và CD. Gọi F là giao điểm của OE và MN. Theo nhận xét trên ta có OF⊥MN và F là điểm Miquel của tứ giác toàn phần ABCDMN. Từ đó ta có tứ giác FDAN nội tiếp.
Theo tính chất phương tích ta có P, Q, M thẳng hàng.
Ta có MF.MN = MA.MD = MQ.MP, suy ra tứ giác PQFN nội tiếp. Do đó góc NQP = góc NFP = 900 . Vậy Q thuộc đường tròn đường kính MNcố định.
b. Tương tự câu a, ta có MR⊥NP tại R. Xét tam giác PMN có các đường cao MR, NQ, PF đồng quy.
Gọi L là giao điểm của QR và MN. Ta có (LF, MN) = −1 , mà M, N, F cố định nên L cố định. Vậy QR luôn đi qua điểm L cố định.
2. Bài tập tự luyện thêm
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O), trực tâm H. Trung tuyến AM cắt (O) lần thứ hai tại N.AH cắt (O) tại K. Các đường
thẳng KN, BC và đường thẳng qua H vuông góc với AN cắt nhau tạo thành tam giác XYZ. Chứng minh rằng (XYZ) tiếp xúc với (O).
Bài 2. Cho tam giác ABC. Một đường tròn Oa qua B, C cắt AC, AB lần lượt tại E, F.BE giao CF tại P. Gọi M là trung điểm của BC, L đối xứng với K qua M. Các đường thẳng PK, QL, BC cắt nhau tạo thành tam giác XYZ. Chứng minh rằng (XYZ) tiếp xúc với (ABC).
Bài 3. Cho tam giác ABC nội tiếp đường tròn (O). Gọi A0 là điểm đối xứng của A qua O. Trung tuyến AM của tam giác ABC cắt BA0 , CA0
lần lượt tại L và K. Các đường thẳng qua L vuông góc với BA0, qua K và vuông góc với CA0 và đường thẳng OM cắt nhau tạo
thành tam giác XYZ. Gọi P là giao của hai tiếp tuyến tại B và C của (O). Chứng minh rằng (AMP) tiếp xúc với (XYZ).
Bài 4. Cho tứ giác lưỡng tâm ABCD có tâm đường tròn ngoại tiếp là O. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC. Chứng minh rằng tồn tại môt đường tròn tâm O tiếp xúc với bốn đường tròn ngoại tiếp các tam giác EAD, EBC, FAB, FCD.
Bài 5. Cho tam giác ABC nội tiếp đường tròn (O) với trực tâm H. Hai đường thẳng d1 và d2 bất kì vuông góc với nhau và đi qua H.d1 cắt BC, CA, AB lần lượt tại X1,Y1, Z1. GọiA1B1C1 là tam giác tạo bởi các đường thẳng qua X1 và vuông góc với BC, qua Y1 và vuông góc CA, qua Z1 và vuông góc với AB. Tương tự ta xác định được tam giác A2B2C2. Chứng minh rằng đường tròn ngoại tiếp các tam giác A1B1C1 và A2B2C2 tiếp xúc với nhau tại một điểm trên (O).
Vậy là các bạn vừa được tìm hiểu Định lí Miquel, tính chất liên quan và một số bài tập áp dụng. Hi vọng, bài viết đã cung cấp thêm cho bạn nguồn tư liệu cần thiết giúp các bạn dạy và học tốt hơn. Xem thêm chuyên đề về định lí Thales trong không gian nữa bạn nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





