Định lí Thales trong tam giác, những hệ quả quan trọng và cách ứng dụng

Định lí Thales trong tam giác, những hệ quả quan trọng và cách ứng dụng

Định lý Thales nói chung, định lí Thales trong tam giác nói riêng là một định lý rất quan trọng trong hình học không gian của nhà toán học người Hy Lạp Thales. Định lí này học sinh đã được tìm hiểu trong chương trình Hình học 8. Nhằm giúp các bạn hệ thống lại tất cả kiến thức cần ghi nhớ về chuyên đề này, về những hệ quả quan trọng và cách ứng dụng định lí Thales trong tam giác để giải toán cực hay, đã chia sẻ bài viết sau đây.

I. LÝ THUYẾT VỀ ĐỊNH LÍ THALES TRONG TAM GIÁC

1. Định lí Thales trong tam giác

Bạn đang xem: Định lí Thales trong tam giác, những hệ quả quan trọng và cách ứng dụng

Định lí Ta lét trong tam giác được phát biểu rằng khi có 1 đường thẳng song song với 1 cạnh của tam giác, đồng thời cắt 2 cạnh còn lại thì sẽ định ra trên 2 cạnh được cắt đó những đoạn thẳng có tỷ lệ tương ứng nhau.

Trong △ABC, đoạn thẳng B’C’ // BC thì ta sẽ có 

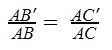
2. Định lý Thales đảo

Định lý Ta lét trong tam giác là một định lý mang tính chất 2 chiều, đó là chiều thuận và chiều đảo ngược.

Định lý Ta lét đảo được phát biểu như sau: Nếu trong một tam giác, một đường thẳng cắt 2 cạnh của tam giác đó và định ra trên 2 cạnh được cắt những đoạn thẳng tương ứng tỉ lệ với nhau thì đường thẳng đó sẽ song song với cạnh còn lại.

Trong △ABC, 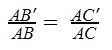thì ta sẽ có B’C’ // BC.

II. NHỮNG HỆ QUẢ CỦA ĐỊNH LÍ THALES – ĐỊNH LÍ THALES MỞ RỘNG

1. Hệ quả 1

Hệ quả đầu tiên của định lí Ta lét trong tam giác đã được phát biểu như sau: Khi một đường thẳng song song với một cạnh của một tam giác có sẵn, đồng thời cắt 2 cạnh còn lại thì sẽ tạo ra được một tam giác mới với ba cạnh tỉ lệ với ba cạnh của tam giác đã được cho trước.

Trong △ABC, đường thẳng DE // BC thì ta sẽ có

Đặc biệt, hệ quả 1 vẫn đúng đối với trường hợp có một đường thẳng a song song với 1 cạnh của tam giác đã cho và cắt 2 cạnh còn lại của tam giác khi kéo dài.

2. Hệ quả 2

Người ta phát biểu hệ quả 2 của định lý Ta lét như sau: Khi một đường thẳng cắt ngang 2 cạnh của một tam giác đã cho trước và song song với cạnh còn lại thì sẽ tạo ra được 1 tam giác mới và tam giác này đồng dạng với tam giác đã được cho trước.

3. Hệ quả 3

Hệ quả 3 của định lí Ta lét trong tam giáccòn được biết đến là một định lý Ta lét mở rộng. Người ta phát biểu định lý mở rộng như sau: Khi ba đường thẳng đồng quy thì sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ.

III. ỨNG DỤNG ĐỊNH LÍ THALES TRONG TAM GIÁC GIẢI BÀI TẬP

Bài 1: Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C vẽ hai đường thẳng song song cắt Ay lần lượt ở D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax ở F.

a) So sánh và ; 

b) Chứng minh rằng: AC²= AB.AF

Bài 2: Cho G là trọng tâm tam giác ABC. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh rằng : BD = 1/3 BC

Bài 3: Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và O.

Chứng minh rằng . 

Bài 4: Cho tam giác ABC có AM là đường trung tuyến. N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC.  Chứng minh rằng .

Bài 5: Cho tam giác vuông cân ABC có góc C = 90⁰.Từ C kẻ một tia vuông góc với trung tuyến AM cắt AB ở D. Hãy tính tỉ số . 

Bài 6: Cho điểm E thuộc cạnh AC của DABC . Qua B kẻ một đường thẳng I.Đường thẳng qua E và song song với BC cắt I tại N. Đường thẳng qua E và song song với AB cắt I tại M. Chứng minh rằng AN // CM.

Bài 7: Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý . Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD.

Bài 8: Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm DABC. Nối GC cắt MN tại O . Chứng minh rằng : OC = 3 OG

Bài 9 : Cho hình thang ABCD ( AB // CD ) với AB = a ; CD = b. Gọi I là giao điểm của hai đường chéo . Đường thẳng qua I và song song với AB cắt hai cạnh bên tại E và F. Chứng minh rằng :

Bài 10:. Hình bình hành ABCD. Gọi M là một điểm trên đường chéo AC. Vẽ ME vuông góc với AB và MF vuông góc với AD. Chứng minh rằng :

Bài 11: Hình thang ABCD đáy lớn CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K ; I thuộc CD). Chứng minh rằng:

a)EF // AB

AB²= CD . EF.

Bài 12: Cho 1 điểm M nằm trong DABC. Đường thẳng  qua M và trọng tâm G của tam giác cắt BC; CA và AB theo thứ tự D, E, F. Chứng minh rằng  

Bài 13: Cho tam giác ABC, trọng tâm G, đường thẳng ( d) qua G cắt các cạnh AB và AC tại M và N. Chứng minh rằng : AM. AN = AM. NC + AN . MB.

Bài 14: Cho tam giác ABC vuông tại A. Giả sử đường cao AH, trung tuyến BM, và phân giác trong CN đồng quy. Chứng minh rằng BH = AC.

Vậy là các bạn vừa được tìm hiểu Định lí Thales trong tam giác, những hệ quả quan trọng và cách ứng dụng vào bài toán cực hay. Hi vọng, bài viết đã cung cấp thêm cho bạn nhiều nguồn tư liệu thiết yếu giúp bạn dạy và học tốt hơn. Xem đầy đủ định lí Thales tai đường link này nhé !