Các phương pháp phân tích đa thức thành nhân tử và các dạng toán
Phân tích đa thức thành nhân tử học sinh đã được tìm hiểu trong chương trình Toán 8. Đây là một trong những phần kiến thức trọng tâm của chương trình. Bài viết hôm nay, .vn sẽ tổng hợp các phương pháp phân tích đa thức thành nhân tử chi tiết nhất. Bạn chia sẻ để nắm vững hơn phương pháp này nhé !
I. CÁC PHƯƠNG PHÁP PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ

Bạn đang xem: Các phương pháp phân tích đa thức thành nhân tử và các dạng toán
Phương pháp 1: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:
Phương pháp :
– Trong đa thức có nhiều hạng tử, ta tìm xem chúng có nhân tử chung là gì.
– Phân tích mỗi hạng tử thành tích của nhân tử chung và nhân tử khác.
– Đặt nhân tử chung ra ngoài, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng).
Ví dụ:
Phương pháp 2: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Phương pháp : Biến đổi đa thức bạn đầu về dạng quen thuộc của hằng đẳng thức, sau đó sử dụng hằng đẳng thức để làm xuất hiên nhân tử chung.
Ví dụ: Phân tích đa thức sau thành nhân tử bằng phương pháp dùng hằng đẳng thức.
a.
Phương pháp 3: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
Phương pháp:
Dùng các tính chất giao hoán, kết hợp của phép cộng các đa thức, ta kếp hợp những hạng tử của đa thức thành từng nhóm thích hợp rồi dùng các phương pháp khác phân tích nhân tử theo từng nhóm rồi phân tích chung đối với các nhóm. Thường sau khi nhóm chúng ta sẽ sử dụng phương pháp đặt nhân tử chung hoặc dùng hằng đắng thức để làm tiếp.
Ví dụ: Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm nhiều hạng tử.
Phương pháp 4: Phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử
Phương pháp:
Vận dụng thêm bớt hạng tử linh hoạt để đưa về nhóm hạng tử chung hoặc dùng hằng đẳng thức
* Ví dụ: Phân tích các đa thức sau thành nhân tử

Phương pháp 5: Phân tích đa thức thành nhân tử bằng phương pháp thêm, bớt một hạng tử
Ta có thể thêm bớt 1 hạng tử nào đó của đa thức để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được.
Ví dụ
Phương pháp 6: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
Trong một số trường hợp, để việc phân tích đa thức thành nhân tử được thuận lợi, ta phải đặt biến phụ thích hợp.
Ví dụ: Phân tích các đa thức sau thành nhân tử
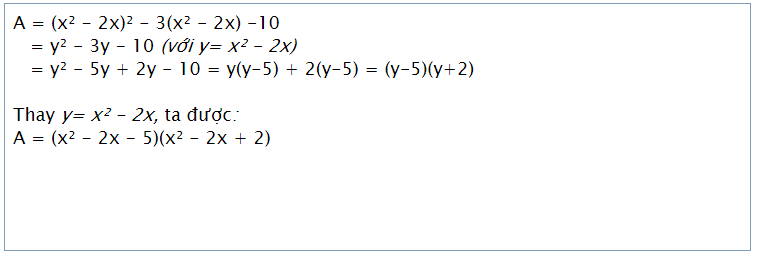
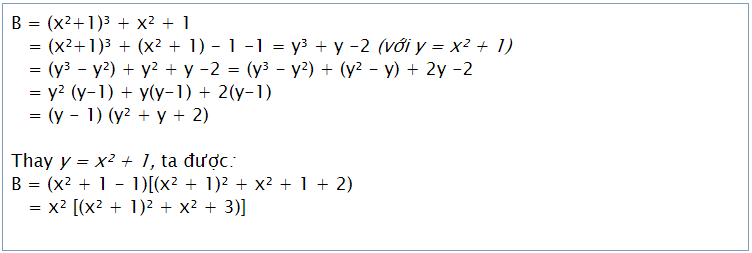
II. CÁC DẠNG TOÁN VẬN DỤNG PHƯƠNG PHÁP PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
Bài 1 : Phân tích đa thức thành nhân tử.
a) 4x2– 1
b) 25x2– 0,09
c) 9x2 –
d) (x – y)2– 4
e) 9 – (x – y)2
f) (x2 + 4)2 – 16x2
Bài 2: Giải phương trình sau :
2(x + 3) – x(x + 3) = 0
Vậy nghiệm của phương trình là x1 = –3: x2 = 2
Bài 3: Phân tích đa thức sau thành nhân tử:
a)8x3+ 4x2 – y3 – y2 = (8x3 – y3) + (4x2 – y2)
b) x2+ 5x –6 = x2 + 6x – x – 6
= x(x + 6) – (x + 6)
= (x + 6)(x – 1)
c. a4 + 16 = a4+ 8a2 + 16 – 8a2
= (a2 + 4)2 – (a)2
= (a2 + 4 +a)( a2 + 4 – a)
Bài 4: Thực hiện phép chia đa thức sau đây bằng cách phân tích đa thức bị chia thành nhân tử:
a) (x5+ x3+ x2 + 1):(x3 + 1)
b) (x2–5x + 6):(x – 3)
Giải:
a) Vì x5+ x3+ x2 + 1
= x3(x2 + 1) + x2 + 1
= (x2 + 1)(x3 + 1)
nên (x5 + x3 + x2 + 1):(x3 + 1)
= (x2 + 1)(x3 + 1):(x3 + 1)
= (x2 + 1)
b)Vì x2 – 5x + 6
= x2 – 3x – 2x + 6
= x(x – 3) – 2(x – 3)
= (x – 3)(x – 2)
nên (x2 – 5x + 6):(x – 3)
= (x – 3)(x – 2): (x – 3)
= (x – 2)
Bài 6: Phân tích các đa thức sau thành nhân tử :
a) 14x2– 21xy2+ 28x2y2 = 7x(2x – 3y2 + 4xy2)
b) 2(x + 3) – x(x + 3) = (x+3)(2-x)
c) x2+ 4x – y2+ 4 = (x + 2)2 – y2 = (x + 2 – y)(x + 2 + y)
Bài 7 : Phân tích đa thức sau thành nhân tử.
a) x4+ 2x2 + 1
b) 4x2 – 12xy + 9y2
c) -x2– 2xy – y2
d) (x + y)2 – 2(x + y) + 1
e) x3– 3x2+ 3x – 1
g) x3 + 6x2 + 12x + 8
h) x3+ 1 – x2 – x
k) (x + y)3 – x3 – y3
Bài 8: Phân tích đa thức sau thành nhân tử :
a) 4x – 4y + x2– 2xy + y2
b) x4 – 4x3 – 8x2 + 8x
c) x3+ x2– 4x – 4
d) x4 – x2 + 2x – 1
e) x4+ x3+ x2 + 1
f) x3 – 4x2 + 4x – 1
Bài 9: Phân tích đa thức sau thành nhân tử :
a) x3+ x2y – xy2 – y3
b) x2y2 + 1 – x2 – y2
c) x2– y2– 4x + 4y
d) x2 – y2 – 2x – 2y
e) x2– y2– 2x – 2y
f) x3 – y3 – 3x + 3y
Bài 10: Tìm x, biết.
a)x3– x2 – x + 1 = 0
b) (2x3 – 3)2 – (4x2 – 9) = 0
c) x4+ 2x3– 6x – 9 = 0
d) 2(x + 5) – x2 – 5x = 0
Bài 11: Tìm giá trị nhỏ nhất của biểu thức :
a. A = x2– x + 1
b. B = 4x2+ y2 – 4x – 2y + 3
c. C = x2+ x + 1
d) D = x2 + y2 – 4(x + y) + 16
e) E = x2 + 5x + 8
g) G = 2x2 + 8x + 9
Bài 12 : Tìm giá trị lớn nhất của biểu thức :
a. A = -4x2– 12x
b) B = 3 – 4x – x2
c) C = x2 + 2y2+ 2xy – 2y
d) D = 2x – 2 – 3x2
e) E = 7 – x2– y2– 2(x + y)
Bài 13: Phân tích các đa thức sau thành nhân tử
1) x2 + 2xy – 8y2 + 2xz + 14yz – 3z2
2) 3x2 – 22xy – 4x + 8y + 7y2 + 1
3) 12x2 + 5x – 12y2 + 12y – 10xy – 3
4) 2x2 – 7xy + 3y2 + 5xz – 5yz + 2z2
5) x2 + 3xy + 2y2 + 3xz + 5yz + 2z2
6) x2 – 8xy + 15y2 + 2x – 4y – 3
7) x4 – 13x2 + 36
8) x4 + 3x2 – 2x + 3
9) x4 + 2x3 + 3x2 + 2x + 1
Bài 14: Phân tích các đa thức sau thành nhân tử
1) (a – b)3 + (b – c)3 + (c – a)3
2) (a – x)y3 – (a – y)x3 – (x – y)a3
3) x(y2 – z2) + y(z2 – x2) + z(x2 – y2)
4) (x + y + z)3 – x3 – y3 – z3
5) 3x5 – 10x4 – 8x3 – 3x2 + 10x + 8
6) 5x4 + 24x3 – 15x2 – 118x + 24
7) 15x3 + 29x2 – 8x – 12
8) x4 – 6x3 + 7x2 + 6x – 8
9) x3 + 9x2 + 26x + 24
Vậy là các bạn vừa được chia sẻ các phương pháp phân tích đa thức thành nhân tử và các dạng toán thường gặp. Hi vọng, những thông tin này hữu ích với bạn. Xem thêm 7 hằng đẳng thức đáng nhớ nữa bạn nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





