Công thức tính toạ độ trung điểm của đoạn thẳng chuẩn xác

Công thức tính toạ độ trung điểm của đoạn thẳng chuẩn xác

Bài viết hôm nay. sẽ giới thiệu cùng quý thầy cô và các em học sinh công thức tính toạ độ trung điểm của đoạn thẳng và nhiều kiến thức liên quan khác trong chuyên đề này. Hãy dành thời gian chia sẻ để nắm chắc hơn phần kiến thức Hình học 9 vô cùng quan trọng này nhé !

I. CÁCH TÍNH TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG

1. Công thức:

Bạn đang xem: Công thức tính toạ độ trung điểm của đoạn thẳng chuẩn xác

Cho hai điểm phân biệt A với B với A(x_A, y_B) và B(x_A, y_B). Khi đó

– Độ dài đoạn thẳng AB được tính bởi công thức

– Tọa độ trung điểm M của AB được tính bởi công thức

2. Ví dụ minh họa

Trong mặt phẳng tọa độ Oxy, cho hai điểm M(2; 9) và N(1; -3). Xác định tọa độ trung điểm I của đoạn thẳng MN.

Hướng dẫn giải:

Tọa độ trung điểm I của MN là

II. CÁC BÀI TOÁN THƯỜNG GẶP TÍNH TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG

Bài 1: Cho tam giác ABC, có B(9; 7) và C(11; -1). Gọi M và N lần lượt là trung điểm của AB và AC. Tọa độ vecto 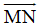 là: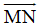

A. (2 ; -8)

B. 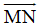(1; -4)

C. 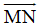(10; 6)

D. 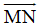(5; 3)

Hướng dẫn giải:

Do M là trung điểm của AB nên ta có: 

Do N là trung điểm của AC nên ta có: 

Tọa độ của 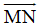 = (x_N; x_M; y_N; y_M)

Vậy 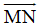 =(1; -4).

Bài 2: Trong mặt phẳng tọa độ Oxy, gọi B’, B”, B”’ lần lượt là điểm đối xứng của B(-2; 7) qua trục Ox, Oy và qua gốc tọa độ O. Tọa độ các điểm B’, B”, B”’ là:

A. B’(-2; -7), B”(2; 7), B”’(2; -7)

B. B’(-7; 2), B”(2; 7), B”’(2; -7).

C. B’(-2; -7), B”(2; 7), B”’(-7; -2)

D. B’(-2; -7), B”(7; 2), B”’(2; -7).

Hướng dẫn giải:

+ B’ đối xứng với B(-2; 7) qua trục Ox, suy ra B’(-2; -7) (do đối xứng qua trục Ox thì hoành độ giữ nguyên và tung độ đối nhau).

+ B” đối xứng với B qua trục Oy, suy ra B”(2; 7) (do đối xứng qua trục Oy thì tung độ giữ nguyên và hoành độ đối nhau).

+ B”’ đối xứng với B qua gốc tọa độ O, suy ra O là trung điểm của BB”’

Nên ta có:  B”’(2; -7)

Đáp án A

Bài 3: Ví dụ 2. Trong mặt phẳng tọa độ Oxy, cho điểm A(2; 3) và B(11; 5). Gọi H là điểm đối xứng của B qua A. Tọa độ điểm H là:

A. H (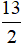; 4)

B. H(-7; 1)

C. H(7; -1)

D. H(20; 7)

Hướng dẫn giải:

Vì H là điểm đối xứng của B qua A, do đó A là trung điểm của BH.

Gọi tọa độ của H là H(x_H; y_H)

Áp dụng công thức tọa độ trung điểm ta có:

 H (-7; 1)

Đáp án B

Bài 4: Cho E(1; -3). Điểm 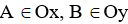 sao cho A là trung điểm của BE. Tọa độ điểm B là:

A. B(0; 3)

B. B(; 0)

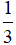
C. B(0; 2)

D. B(4; 2)

Hướng dẫn giải:

Ta có: 

Do A là trung điểm của BE nên ta có 

Vậy B(0; 3).

Đáp án A

Vậy là các bạn vừa được tìm hiểu cách tính toạ độ trung điểm của đoạn thẳng và nhiều kiến thức liên quan khác trong chuyên đề này. Hi vọng, chia sẻ cùng bài viết, bạn đã nắm vững hơn phần kiến thức Hình học 9 quan trọng này. Xem thêm công thức bất đẳng thức Bunhiacopxki tại đường link này nhé !

Giáo dục