Phương trình đường tròn: lý thuyết, công thức và cách giải các dạng toán
Phương trình đường tròn: lý thuyết, công thức và cách giải các dạng toán là phần kiến thức Toán 10, phân môn Hình học vô cùng quan trọng. Nhằm giúp quý thầy cô và các bạn học sinh có thêm nguồn tư liệu quý trong việc dạy và học, đã chía sẻ bài viết sau đây. Cùng tìm hiểu nhé !
I. LÝ THUYẾT VỀ PHƯƠNG TRÌNH ĐƯỜNG TRÒN
1. Lập phương trình đường tròn có tâm và bán kính cho trước
Bạn đang xem: Phương trình đường tròn: lý thuyết, công thức và cách giải các dạng toán
Phương trình đường tròn có tâm , bán kính R là :
=R2
2. Nhận xét
Phương trình đường tròn =R2 có thể được viết dưới dạng
trong đó
Ngược lại, phương trình là phương trình của đường tròn khi và chỉ khi . Khi đó đường tròn(C) có tâm và bán kính
3. Phương trình tiếp tuyến của đường tròn
Cho điểm nằm trên đường tròn tâm .Gọi là tiếp tuyến với (C) tại
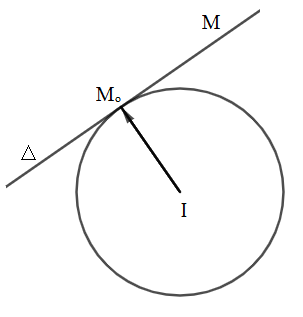
Ta có thuộc và vectơ là vectơ pháp tuyến cuả
Do đó có phương trình là:
Phương trình này là phương trình tiếp tuyến của đường tròn tại điểm nằm trên đường tròn.
II. CÁC DẠNG TOÁN VỀ PHƯƠNG TRÌNH ĐƯỜNG TRÒN VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Lập phương trình đường tròn
Cách giải 1:
- Tìm tọa độ tâm I(a; b) của đường tròn (C)
- Tìm bán kính R của (C)
- Viết phương trình (C) theo dạng: (x – a)2 + (y – b)2 = R2 (1)
Chú ý:
- (C) đi qua A, B ⇔ IA2 = IB2 = R2.
- (C) đi qua A và tiếp xúc với đường thẳng ∆ tại A ⇔ IA = d(I, ∆).
- (C) tiếp xúc với hai đường thẳng ∆1 và ∆2
⇔ d(I, ∆1) = d(I, ∆2) = R
Cách giải 2:
- Gọi phương trình đường tròn (C) là x2 + y2 – 2ax – 2by + c = 0 (2)
- Từ điều kiện của đề bài đưa đến hệ phương trình với ba ẩn số là: a, b, c
- Giải hệ phương trình tìm a, b, c để thay vào (2), ta được phương trình đường tròn (C)
Dạng 2: Lập phương trình tiếp tuyến của đường tròn
Loại 1: Lập phương trình tiếp tuyến tại điểm Mo(xo;yo) thuộc đường tròn (C)
- Tìm tọa độ tâm I(a,b) của đường tròn (C)
- Phương trình tiếp tuyến với (C) tại Mo(xo;yo) có dạng:
Loại 2: Lập phương trình tiếp tuyến của ∆ với (C) khi chưa biết tiếp điểm: dùng điều kiện tiếp xúc với đường tròn (C) tâm I, bán kính R ⇔ d (I, ∆) = R
Dạng 3: Nhận dạng một phương trình bậc 2 là phương trình đường tròn. Tìm tâm và bán kính của đường tròn
Cách giải 1:
- Đưa phương trình về dạng: x2 + y2 – 2ax – 2by + c = 0 (1)
- Xét dấu biểu thức:
- Nếu M thì (1) là phương trình đường tròn tâm I(a;b), bán kính
Cách giải 2:
Đưa phương trình về dạng: (x – a)2 + (y – b)2 = m(2)
Nếu m thì (2) là phương trình đường tròn tâm I(a;b), bán kính
III. BÀI TẬP VỀ PHƯƠNG TRÌNH ĐƯỜNG TRÒN
Bài 1 (trang 83 SGK Hình học 10): Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y – 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 – 4x + 6y – 3 = 0
Lời giải

Bài 2 (trang 83 SGK Hình học 10): Lập phương trình đường tròn (C) trong các trường hợp sau:
a, (C) có tâm I(-2; 3) và đi qua M(2; -3);
b, (C) có tâm I(-1; 2) và tiếp cúc với đường thẳng x – 2y +7 =0
c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).
Lời giải

Bài 3 (trang 84 SGK Hình học 10): Lập phương trình đường tròn đi qua ba điểm:
a, A(1; 2), B(5; 2), C(1; -3)
b, M(-2; 4), N(5; 5), P(6; -2)
Lời giải

Bài 4 (trang 84 SGK Hình học 10): Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và qua điểm M(2; 1).
Lời giải

Bài 5 (trang 84 SGK Hình học 10): Lập phương trình của đường tròn tiếp xúc với các trục tọa độ và có tâm nằm trên đường thẳng 4x – 2y – 8 = 0
Lời giải

Vậy là đã gửi tới quý thầy cô cùng các bạn chuyên đề về phương trình đường tròn: lý thuyết, công thức và cách giải các dạng toán. Hi vọng, đây sẽ là nguồn tư liệu hữu ích giúp các bạn dạy và học tốt hơn. Cảm ơn các bạn đã theo dõi bài viết ! Xem thêm cách viết phương trình tham số tại đường link này nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





