Tìm hiểu cách tính đạo hàm của hàm hợp cực hay và cực dễ

Để tiếp tục mạch kiến thức cách tính đạo hàm của các hàm số thường gặp, hôm nay, sẽ chia sẻ cùng quý thầy cô và các bạn lý thuyết về đạo hàm của hàm số hợp cùng cách tính đạo hàm của hàm hợp cực hay và chi tiết. Chia sẻ ngay để có thêm nguồn tư liệu quý phục vụ quá trình dạy và học bạn nhé !

I. LÝ THUYẾT VỀ ĐẠO HÀM CỦA HÀM HỢP

1. Đạo hàm của hàm số hợp là gì?

Bạn đang xem: Tìm hiểu cách tính đạo hàm của hàm hợp cực hay và cực dễ

Giả sử phương trình 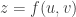$mathop z = f(u,v)$ (1) xác định với u, v là hàm số của các biến độc lập x và y: $u = g(x,y) , v = h(x,y)$ (2) thì khi đó z được gọi là hàm số hợp của các biến số x và y thông qua 2 biến trung gian u và v.

Như vậy z cũng có thể biểu diễn như hàm 2 biến x, y: $z = f(g(x,y);h(x,y))$ (3)

Ví dụ: Cho $z = uv + u^v ; u = sin(x+y) , v = sqrt{x^2+y^2}$

Khi đó: $z = sin(x+y).{sqrt{x^2+y^2}}+(sin(x+y))^{sqrt{x^2+y^2}}$

Tình huống:

Nếu ta cần khảo sát đạo hàm của hàm số hợp thì có thể viết hàm số dưới dạng tường minh theo 2 biến x, y. Tuy nhiên, với hàm trên thì việc lấy đạo hàm riêng sẽ rất khó khăn. Hoặc nếu hàm số chưa xác định được công thức, ví dụ: $z = f(x+y;xy)$ hoặc $z = sin(u(x,y);v(x,y))$ thì làm sao tính được các đạo hàm riêng.

2. Định lý: (Tính ${ dfrac{partial z}{partial x}} , { dfrac{partial z}{partial y}}$ từ (1), (2) mà không dùng (3)

Cho z = f(u,v) và u, v là các hàm của hai biến u = u(x,y) và v = v(x,y). Cho các hàm z, u, v khả vi tại các điểm tương ứng. Khi đó, z = f(u,v) có các đạo hàm riêng ${ dfrac{partial z}{partial x}} , { dfrac{partial z}{partial y}}$ xác định bởi công thức:

${ dfrac{partial z}{partial x}}= { dfrac{partial z}{partial u}}.{ dfrac{partial u}{partial x}} + { dfrac{partial z}{partial v}}.{ dfrac{partial v}{partial x}}$ ; ${ dfrac{partial z}{partial y}}= { dfrac{partial z}{partial u}}.{ dfrac{partial u}{partial y}} + { dfrac{partial z}{partial v}}.{ dfrac{partial v}{partial y}}$

II. CÁCH TÍNH ĐẠO HÀM CỦA HÀM HỢP CỰC HAY

1. Một số trường hợp tổng quát

1. Với z = f(u,v, w) , trong đó u = u(t), v = v(t), w = w(t)

Khi đó: z là hàm số hợp của 1 biến số t thông qua 3 biến trug gian u, v, w.

Bấy giờ, đạo hàm của z theo t được xác định

${ dfrac{dz}{dt}} = { dfrac{partial z}{partial u}}.{ dfrac{du}{dt}} + { dfrac{partial z}{partial v}}.{ dfrac{dv}{dt}} + { dfrac{partial z}{partial w}}.{ dfrac{dw}{dt}}$

(do z, u, v, w đều là hàm theo 1 biến t nên đạo hàm là đạo hàm thường)

Áp dụng: tính ${ dfrac{du}{dt}}$ , nếu $z = xyz$ , với $x = t^2 + 1 , y = lnt , z = tgt$

Tương tự quy tắc trên, ta có: ${ dfrac{du}{dt}} = { dfrac{partial u}{partial x}}.{ dfrac{dx}{dt}} + { dfrac{partial u}{partial y}}.{ dfrac{dy}{dt}} + { dfrac{partial u}{partial z}}.{ dfrac{dz}{dt}}$

Nghĩa là: ${ dfrac{du}{dt}} = yz.2t + xz.{ dfrac{1}{t}} + xy.(1+tg^2t)$

Hay: ${ dfrac{du}{dt}} = 2t.lnt.tgt + { dfrac{(t^2+1).tgt}{t}} + (t^2+1).lnt.(1+tg^2t)$

Ví dụ 1: Tính ${ dfrac{dz}{dx}} , { dfrac{partial z}{partial x}}$ nếu $z = y^x$ với y = f(x).

Trong ví dụ này, ta cần chú ý và phân biệt ý nghĩa của hai ký hiệu ${ dfrac{dz}{dx}} , { dfrac{partial z}{partial x}}$

Đầu tiên, ký hiệu ${ dfrac{dz}{dx}}$ chỉ z là hàm theo 1 biến x, trong khi đó, biểu thức xác định của z là: $z = y^x , y = f(x)$ nên với ký hiệu này ta sẽ hiểu là z là hàm số hợp của 1 biến x thông qua biến trung gian y.

Còn ký hiệu, $dfrac{partial z}{partial x}$ chỉ đạo hàm riêng của z theo biến x, điều này được hiểu là z là hàm hai theo 2 biến độc lập x, y.

Như vậy: ${ dfrac{partial z}{partial x}} = y^x.lny$

Còn: ${ dfrac{dz}{dx}} = { dfrac{partial z}{partial x}} + { dfrac{partial z}{partial y}}.{ dfrac{dy}{dx}} = y^x.lny + x.y^{x-1}.f'(x)$

2. Đạo hàm cấp 2 của hàm số hợp 2 biến

Giả sử z là hàm số hợp theo 2 biến x, y thông qua 2 biến trung gian u, v. Khi đó ta đã có công thức tính đạo hàm riêng cấp 1 của z đối với 2 biến x, y. Vấn đề đặt ra là: vậy nếu cần tính tiếp tục đạo hàm riêng cấp 2 của hàm số hợp thì ta phải làm thế nào?

Ta chú ý, trong công thức: ${ dfrac{partial z}{partial x}}= { dfrac{partial z}{partial u}}.{ dfrac{partial u}{partial x}} + { dfrac{partial z}{partial v}}.{ dfrac{partial v}{partial x}}$

Các đại lượng ${ dfrac{partial z}{partial u}}, { dfrac{partial z}{partial v}}$ lại là các biểu thức theo u, v nên nó lại là những hàm số hợp của hai biến x, y thông qua 2 biến trung gian u, v.

Do đó: ${ dfrac{{partial}^2z}{partial x^2}} = left( { dfrac{partial z}{partial u}}.{ dfrac{partial u}{partial x}} + { dfrac{partial z}{partial v}}.{ dfrac{partial v}{partial x}} right)_x^{'}$

$= left({ dfrac{partial z}{partial u}} right)_x^{'}.{ dfrac{partial u}{partial x}} + { dfrac{partial z}{partial u}}.{ dfrac{{partial}^2u}{partial x^2}} + left({ dfrac{partial z}{partial v}} right)_x^{'}.{ dfrac{partial v}{partial x}} + { dfrac{partial z}{partial v}}.{ dfrac{{partial}^2v}{partial x^2}}$ (*)

Mặt khác, áp dụng quy tắc tính đạo hàm hàm số hợp cho 2 hàm ${ dfrac{partial z}{partial u}}, { dfrac{partial z}{partial v}}$ . Ta có:

$left({ dfrac{partial z}{partial u}} right)_x^{'} = { dfrac{{partial}^2z}{partial u^2}}.{ dfrac{partial u}{partial x}} + { dfrac{{partial}^2z}{{partial}u{partial}v}}.{ dfrac{partial v}{partial x}}$ , $left({ dfrac{partial z}{partial v}} right)_x^{'} = { dfrac{{partial}^2z}{{partial}v{partial}u}}.{ dfrac{partial u}{partial x}} + { dfrac{{partial}^2z}{partial v^2}}.{ dfrac{partial v}{partial x}}$ (**)

Từ (*), (**) ta có:

${ dfrac{{partial}^2z}{partial x^2}} = z_{uu}^{''}. left(u_x^{'}right)^2 + 2.z_{uv}^{''}.u_x^{'}.v_x^{'} + z_{vv}^{''}. left( v_x^{'} right)^2 + z_u^{'}.u_{xx}^{''} + z_v^{'}.v_{xx}^{''}$

Hoàn toàn tương tự, ta tìm được công thức xác định ${ dfrac{{partial}^2z}{{partial}x{partial}y}} , { dfrac{{partial}^z}{{partial}y^2}}$

III. BÀI TẬP TÍNH ĐẠO HÀM CỦA HÀM HỢP

Bài 1. Tính đạo hàm của hàm số: y= ( 3×2+ 5x- 10)⁷

A. 7.( 3x²+5x-10)⁶

B. ( 3x²+5x-10)⁶.( 6x+5)

C. 7.( 3x²+5x-10)⁶.( 6x+5)

D. Đáp án khác

Hướng dẫn giải

Đạo hàm của hàm số đã cho là:

y’=7.( 3x²+5x-10)⁶.(3x²+5x-10)’

y’= 7.( 3x²+5x-10)⁶.( 6x+5)

Chọn C.

Bài 2. Đạo hàm của hàm số y = f(x)= ( 1- 3x²,)⁵ là:

A. -30x.(1-3x² )⁴ B. -10x.(1-3x² )⁴

C. 30(1-3x² )⁴ D. -3x.(1-3x²)⁴

Hướng dẫn giải

Đặt u (x)= 1- 3×2 suy ra u (x)=( 1-3x² )’=(1)’-3(x² )’= -6x

Với u= 1-3×2 thì y= u⁵ suy ra y^‘ (u)=5.u⁴=5.(1-3x²)⁴

Áp dụng công thức đạo hàm của hàm hợp ta có :

y^‘ (x)= 5.(1-3x² )⁴.(-6x)= -30x.(1-3x² )⁴

Chọn A.

Bài 4. Tính đạo hàm của hàm số y= ( 2√x+6x-10)²

A. y’=( 2√x+6x-10).( 1/√x+6) B. y’=2.( 2√x+6x-10).( 1/√x+6)

C. y’=2.( 2√x+6x-10).( 2/√x+6) D. Đáp án khác

Hướng dẫn giải

Áp dụng công thức đạo hàm của hàm hợp ; ta có :

y’=2.( 2√x+6x-10).( 2√x+6x-10)’

Hay y’=2.( 2√x+6x-10).( 1/√x+6)

Chọn B.

Bài 5. Tính đạo hàm của hàm số : y= √(x⁴+3x²+2x-1)

Hướng dẫn giải

Áp dụng công thức tính đạo hàm của hàm hợp ta có

Bài 6. Tính đạo hàm của hàm số : y= √((2x-10)⁴+10)

Hướng dẫn giải

Áp dụng công thức đạo hàm của hàm hợp ta có :

Bài 7. Tính đạo hàm của hàm số : y= (-2)/( x³+2x²) + (2x+1)²

Hướng dẫn giải

Áp dụng công thức đạo hàm của hàm hợp ta có :

Bài 8. Tính đạo hàm của hàm số : y=√(x²+2x-10)+( 2x+1)⁴

Hướng dẫn giải

Áp dụng công thức đạo hàm của hàm hợp ta có :

Bài 9. Tính đạo hàm của hàm số : y= ( x³+ x²-1)² ( 2x+1)²

A. y’= ( x³+ x²-1)( 3x²+2x).(2x+1)²+(x³+ x²-1)².( 8x+4)

B. y’= 2( x³+ x²-1)( 3x²+2x).(2x+1)²+(x³+ x²-1)².( 8x+4)

C. y’= ( x³+ x²-1)( 3x²+2x).(2x+1)²+(x³+ x²-1)².( 4x+4)

D. y’= 2( x³+ x²-1)( 3x²+2x).(2x+1)²-(x³+ x²-1)².( 8x+4)

Hướng dẫn giải

áp dụng công thức đạo hàm của của hàm hợp và đạo hàm của một tích ta có :

y’=[( x³+ x²-1) ]²‘.(2x+1)²+(x³+ x²-1)².[(2x+1)²]’

Hay y’=2( x³+ x²-1)( x³+ x²-1)’.(2x+1)²+

(x³+ x²-1)².2( 2x+1).(2x+1)’

⇔ y’= 2( x³+ x²-1)( 3x²+2x).(2x+1)²+(x³+ x²-1)².2( 2x+1).2

⇔ y’= 2( x³+ x²-1)( 3x²+2x).(2x+1)²+(x³+ x²-1)².( 8x+4)

Chọn B.

Bài 10. Tính đạo hàm của hàm số .

Hướng dẫn giải

Bài 11. Tính đạo hàm của hàm số

Hướng dẫn giải

Vậy là các bạn vừa được tìm hiểu lý thuyết về đạo hàm của hàm số hợp cùng cách tính đạo hàm của hàm hợp cực hay và chi tiết. Hi vọng, những thông tin chia sẻ trên đây hữu ích với bạn. Xem thêm cách tính đạo hàm của hàm số lũy thừa nữa bạn nhé !

Giáo dục

Bản quyền bài viết thuộc thcs-thptlongphu. Mọi hành vi sao chép đều là gian lận!

Tác giả: https://thcs-thptlongphu.edu.vn – Trường Lê Hồng Phong

Nguồn: https://thcs-thptlongphu.edu.vn/tim-hieu-cach-tinh-dao-ham-cua-ham-hop-cuc-hay-va-cuc-de/