Giải bài tập trang 147 bài 6 tam giác cân Sách Bài Tập Toán lớp 7 tập 1. Câu 67: Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50°, bằng a °…
Câu 67 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
a) Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50°, bằng a °
b) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 50°, bằng a°
Bạn đang xem: Giải bài 67, 68, 69, 70 trang 147 SBT Toán lớp 7 tập 1
Giải
a) Vì tam giác cân có hai góc ở đáy bằng nhau nên số đo của một góc bằng 180° trừ góc ở đỉnh rồi chia cho 2
Ta có: ({{180^circ – 50^circ } over 2} = 65^circ )
({{180^circ – a^circ } over 2})
b) Vì tam giác cân có hai góc ở đáy bằng nhau nên góc ở đỉnh bằng 180° trừ đi hai lần góc ở đáy.
Ta có: 180 °– 50°. 2 = 180° – 100° = 80°
180° – a . 2
Câu 68 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A có (widehat A = 100^circ). Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC.
Giải
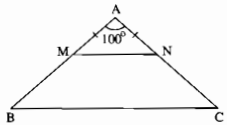
Vì ∆ABC cân tại A nên (widehat B = widehat C)
Ta có: (widehat B = {{180^circ – widehat A} over 2})
( = {{180^circ – 100^circ } over 2} = 40^circ ) (1)
Mà AM = AN (gt) nên ∆AMN cân tại A => (widehat {AMN} = widehat {ANM})
(Rightarrow widehat {AMN} = {{180^circ – widehat A} over 2} = {{180^circ – 100^circ } over 2} = 40^circ ) (2)
Từ (1) và (2) suy ra: (widehat B = widehat {AMN})
Vậy MN // BC (vì có cặp góc ở vị trí đồng vị bằng nhau).
Câu 69 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM = CN.
Giải

Xét ∆ABM và ∆CAN, ta có:
AB = AC (gt)
(widehat A) chung
AM = AN (cùng bằng một nửa AB, AC)
Suy ra: ∆ABM = ∆ACN (c.g.c)
Vậy DM = CN (hai cạnh tương ứng)
Câu 70 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK . Gọi O là giao điểm của BH và CK. Chứng minh rằng ∆OBC là tam giác cân.
Giải

Xét ∆ABH và ∆ACK, ta có:
AB = AC (gt)
(widehat A) chung
AH = AK (gt)
Suy ra: ∆ABH = ∆ACK (c.g.c)
(Rightarrow widehat {{B_1}} = widehat {{C_1}}) (hai góc tương ứng)
(eqalign{
& widehat {ABC} = widehat {{B_1}} + widehat {{B_2}}left( 2 right) cr
& widehat {ACB} = widehat {{C_1}} + widehat {{C_2}}left( 3 right) cr} )
(widehat {ABC} = widehat {ACB}) (tính chất tam giác cân) (4)
Từ (1), (2), (3) và (4) suy ra: (widehat {{B_2}} = widehat {{C_2}}) hay ∆BOC cân tại O.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





