Giải bài 61, 62, 63 trang 145, 146 SBT Toán lớp 7 tập 1

Giải bài tập trang 145, 146 bài 5 trường hợp bằng nhau thứ nhất của tam giác góc-cạnh-góc (g-c-g) Sách Bài Tập Toán lớp 7 tập 1. Câu 61: Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng…

Câu 61 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:

a) ∆BAD = ∆ACE

Bạn đang xem: Giải bài 61, 62, 63 trang 145, 146 SBT Toán lớp 7 tập 1

b) DE = BD + CE

Giải

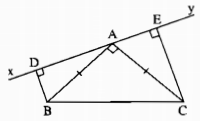
a) Ta có: (widehat {BA{rm{D}}} + widehat {BAC} + widehat {CA{rm{E}}} = 180^circ ) (kề bù)

Mà (widehat {BAC} = 90^circ left( {gt} right) Rightarrow widehat {BA{rm{D}}} + widehat {CA{rm{E}}} = 90^circ )            (1)

Trong ∆AEC, ta có:

(widehat {A{rm{E}}C} = 90^circ  Rightarrow widehat {CA{rm{E}}} + widehat {AC{rm{E}}}{rm{ = 90}}^circ )                   (2)

Từ (1) và (2) suy ra: (widehat {BA{rm{D}}} = widehat {AC{rm{E}}})

Xét hai tam giác vuông AEC và BDA, ta có: 

(widehat {A{rm{E}}C} = widehat {B{rm{D}}A} = 90^circ )

AC = AB (gt)

(widehat {AC{rm{E}}} = widehat {BA{rm{D}}}) (chứng minh trên)

Suy ra:  ∆AEC = ∆BDA (cạnh huyền, góc nhọn)

b) Ta có: ∆AEC = ∆BDA

=> AE = BD và EC = DA

Mà DE = DA + AE

Vậy: DE = CE + BD 

 

---

Câu 62 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác  vuông tại A là ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:

a) DM = AH

b) MN đi qua trung điểm của DE

Giải

a) Ta có (widehat {BAH} + widehat {BA{rm{D}}} + widehat {DAM} = 180^circ ) (kề bù)

Mà  (widehat {BA{rm{D}}} = 90^circ  Rightarrow widehat {BAH} + widehat {DAM} = 90^circ )      (1)

Trong tam giác vuông AMD, ta có:

(widehat {AM{rm{D }}} = 90^circ  Rightarrow widehat {DAM} + widehat {A{rm{D}}M} = 90^circ left( 2 right))

Từ (1) và (2) suy ra: (widehat {BAH} = widehat {A{rm{D}}M})

Xét hai tam giác vuông AMD và BHA, ta có:

(widehat {AM{rm{D}}} = widehat {BAH} = 90^circ )

AB = AD (gt)

(widehat {BAH} = widehat {A{rm{D}}M}) (chứng minh trên)

Suy ra: ∆AMD = ∆BHA (cạnh huyền, góc nhọn)

Vậy: AH = DM (2 cạnh tương ứng)     (3)

b) Ta có: (widehat {HAC} + widehat {CA{rm{E}}} + widehat {E{rm{A}}N} = 180^circ ) (kề bù)

Mà (widehat {CA{rm{E}}} = 90^circ left( {gt} right) Rightarrow widehat {HAC} + widehat {E{rm{A}}N} = 90^circ )     (4)

Trong tam giác vuông AHC, ta có:

(widehat {AHC} = 90^circ  Rightarrow widehat {HAC} + widehat {HCA} = 90^circ left( 5 right))

Từ (4) và (5) suy ra: (widehat {HCA} = widehat {E{rm{A}}N})

Xét hai tam giác vuông AHC và ENA, ta có:

(widehat {AHC} = widehat {E{rm{N}}A} = 90^circ )

AC = AE (gt)

(widehat {HCA} = widehat {E{rm{A}}N}) (chứng minh trên)

Suy ra: ∆AHC = ∆ENA (cạnh huyền, góc nhọn)

Vậy AH = EN (2 cạnh tương ứng)

Từ (3) và (6)  suy ra : DM = EN

Vì (DM bot AH) và (EN bot AH) nên DM // EN (2 đường thẳng cùng vuông góc đường thẳng thứ 3)

Gọi O là giao điểm MN và DE

Xét hai tam giác vuông DMO và ENO, ta có:

(widehat {DMO} = widehat {EN{rm{O}}} = 90^circ )

DM = EN (chứng minh trên)

(widehat {M{rm{D}}O} = widehat {NEO}) (so le trong)

Suy ra: ∆DMO = ∆ENO (g.c.g) => OD = DE

Vậy MN đi qua trung điểm của DE.

 

---

Câu 63 trang 146 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:

a) AD = EF

b) ∆ADE =∆EFC

c) AE = EC

Giải

a) Xét ∆DBF và ∆FDE, ta có ;

(widehat {B{rm{D}}F} = widehat {DF{rm{E}}}) (so le trong vì EF // AB)

DF cạnh chung

(widehat {DFB} = widehat {F{rm{D}}E}) (so le trong vì DE // BC)

Suy ra: ∆DBF = ∆FED(g.c.g) =>DB = EF (2 cạnh tương ứng)

Mà AD = DB (gt)

Vậy: AD  = EF

b) Ta có: DE // BC (gt)

( Rightarrow widehat {{D_1}} = widehat B) (đồng vị)

EF // AB (gt)

( Rightarrow widehat {{F_1}} = widehat B) (đồng vị)

(widehat {{E_1}} = widehat A) (đồng vị)

Xét ∆ADE và ∆ EFC, ta có:

(widehat A = widehat {{E_1}}) (chứng minh trên)

AD = EF (chứng minh trên)

(widehat {{D_1}} = widehat {{F_1}}) (vì cùng bằng (widehat B)) 

Suy ra: ∆ADE = ∆ EFC (g.c.g)

c) Vì ∆ADE = ∆ EFC (chứng minh trên)

Nên AE = EC (hai cạnh tương ứng)

Trường

Giải bài tập