Giải bài tập trang 162 bài 4 Vị trí tương đối của đường thẳng và đường tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 35: Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với các trục tọa độ…
Câu 35 trang 162 Sách bài tập (SBT) Toán 9 Tập 1
Trên mặt phẳng tọa độ cho điểm I có tọa độ ( -3 ; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với các trục tọa độ?
Giải:
Bạn đang xem: Giải bài 35, 36, 37 trang 162 SBT Toán 9 tập 2
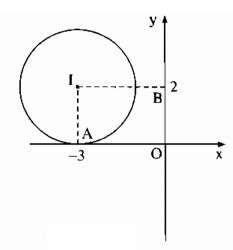
Kẻ IA ⊥ Ox
Ta có: IA = 2 = R
Suy ra đường tròn (I) tiếp xúc với trục hành.
Kẻ IB ⊥ Oy
Ta có: IB = 3 > R
Suy ra đường tròn và trục tung không có điểm chung.
Câu 36 trang 162 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và tiếp xúc với đường thẳng a nằm trên đường nào?
Giải:

Vì đường tròn tâm I bán kính 5cm tiếp xúc với đường thẳng a nên khoảng cách từ I đến a là 5cm.
Vậy I nằm trên hai đường thẳng x và y song song với a, cách a một khoảng bằng 5cm.
Câu 37 trang 162 Sách bài tập (SBT) Toán 9 Tập 1
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm).
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Giải:

a) Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm.
Mà AH = d = 12cm
Nên suy ra d
Vậy ( A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C.
b) Áp dụng định lí Pi-ta-go vào tam giác vuông AHC, ta có:
(A{C^2} = A{H^2} + H{C^2})
Suy ra: (H{C^2} = A{C^2} – A{H^2} = {13^2} – {12^2} = 25 Rightarrow HC = 5(cm))
Ta có: BC = 2.HC = 2.5 = 10 (cm)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





