Giải bài tập trang 68, 69 bài 1 góc ở tâm, số đo cung SGK Toán lớp 9 Tập 2. Câu 1: Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau…
Bài 1 trang 68 sgk Toán lớp 9 Tập 2
Bài 1. Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau:
a) 3 giờ;
Bạn đang xem: Giải bài 1, 2, 3 trang 68, 69 SGK Toán lớp 9 Tập 2
b) 5 giờ;
c) 6 giờ;
d) 12 giờ;
e) 20 giờ.
Hướng dẫn giải:
Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là (360^0: 12 = 30^0)
a) Vào thời điểm 3 giờ thì góc tạo thành giữa hai kim đồng hồ là: (3. 30^0= 90^0)
b) Vào thời điểm 5 giờ thì góc tạo thành giữa hai kim đồng hồ là: (5. 30^0= 150^0)
c) Vào thời điểm 6 giờ thì góc tạo thành giữa hai kim đồng hồ là: (6. 30^0= 180^0)
d) Vào thời điểm 20 giờ thì góc tạo thành giữa hai kim đồng hồ là: (4. 30^0= 120^0)
e) Vào thời điểm 12 giờ hai kim đồng hồ trùng nhau thì góc tạo thành giữa hai kim đồng hồ là: (0^0)
Bài 2 trang 69 sgk Toán lớp 9 tập 2
Bài 2. Cho hai đường thẳng (xy) và st cắt nhau tại (O), trong các góc tạo thành có góc (40^{circ}). Vẽ một đường tròn tâm (O). Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Giải
Ta có (widehat{xOs}) = (40^{circ}) (theo giải thiết)
(widehat{tOy})= (40^{circ})( đối đỉnh với (widehat{xOs}))
(widehat{xOt}) + (widehat{tOy}) = (180^{circ}) nên suy ra
(widehat{xOt})= – (widehat{tOy}) = (180^{circ})- (40^{circ}) = (140^{circ})
(widehat{yOs}) = (140^{circ})(đối đỉnh với (widehat{xOt}))
(widehat{xOy}) = (widehat{sOt}) = (180^{circ})
Bài 3 trang 69 sgk Toán lớp 9 tập 2
Bài 3. Trên các hình 5, 6, hãy dùng dụng cụ đo góc để tìm số đo cung (overparen{AmB}). Từ đó tính số đo cung (overparen{AnB}) tương ứng.
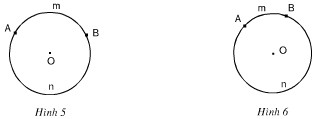
Hướng dẫn giải:

Nối (OA, OB)
Đo góc ở tâm (widehat{AOB}) để suy ra số đo cung (overparen{AmB})
Suy ra (sđoverparen{AnB}= 360^0 – sđ overparen{AmB})
a) Hình a. Ta có: (widehat{AOB} =125^0)
(=> sđoverparen{AmB} = 125^0)
và ( sđoverparen{AnB} = 360^0- 125^0= 235^0)
b) Hình b. Ta có góc (widehat{AOB} = 65^0)
(=> sđoverparen{AmB} = 65^0)
(sđoverparen{AnB} )= ( 360^0) -(sđoverparen{ AmB}) (= 360^0 – 65^0 = 295^0)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





