Giải bài 64, 65, 66 trang 64 SGK Toán 9 tập 2

Giải bài tập trang 64 bài ôn tập chương IV SGK Toán 9 tập 2. Câu 64: Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị…

Bài 64 trang 64 SGK Toán 9 tập 2

Bài 64. Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị, nhưng bạn Quân nhầm đầu bài lại tính tích của một số dương với một số bé hơn nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?

Giải:

Bạn đang xem: Giải bài 64, 65, 66 trang 64 SGK Toán 9 tập 2

Gọi (x) là số dương mà đấu bài cho, (x ∈ N*)

Bạn Quân đã chọn số ((x – 2)) để nhân với (x).

Theo đề bài, ta có: (x(x – 2) = 120) hay (x^2 – 2x – 120 = 0)

Giải phương trình ta được (x = 12) (thỏa mãn) và (x=-10) (loại)

Theo đầu bài yêu cầu tìm tích của (x) với (x +2)

Vậy kết quả đúng phải là: (12.14 = 168)

Bài 65 trang 64 SGK Toán 9 tập 2

Bài 65. Một xe lửa đi từ Hà Nội vào Bình Sơn (Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với vận tốc lớn hơn vận tốc của xe lửa thứ nhất là 5km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng đường Hà Nội – Bình Sơn dài 900km.

Giải:

Gọi (x) (km/h) là vận tốc của xe thứ nhất. Điều kiện (x > 0).

Khi đó vận tốc của xe lửa  thứ hai là (x + 5) (km/h).

Thời gian xe lửa thứ nhất đi từ Hà Nội đến chỗ gặp nhau là: ({{450} over x}) (giờ)

Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là: ({{450} over {x + 5}}) (giờ)

Vì xe lửa thứ hai đi sau (1) giờ, nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe thứ nhất (1) giờ. Ta có phương trình:

({{450} over x} – {{450} over {x + 5}} = 1 Leftrightarrow {x^2} + 5{rm{x}} – 2250 = 0) 

Giải phương trình ta được: ({x_1} = 45) (nhận); ({x_2} = -50) (loại)

Vậy: Vận tốc của xe lửa thứ nhất là (45) km/h

Vận tốc của xe lửa thứ hai là (50) km/h.

Bài 66 trang 64 SGK Toán 9 tập 2

Bài 66. Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm².

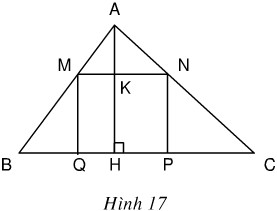
Giải:

Gọi (x) (cm) là độ dài của đoạn (AK). Điều kiện (0

Vì (∆ABC) đồng dạng (∆AMN) nên

(eqalign{
& {{MN} over {BC}} = {{AM} over {AB}} = {{AK} over {AH}} = {x over {12}} cr
& Rightarrow MN = {{16x} over {12}} = {{4{rm{x}}} over 3} cr} )  

Ta có: (MQ = KH = 12 – x)

Do đó diện tich hình chữ nhật (MNPQ) là: (left( {12 – x} right){{4{rm{x}}} over 3}) 

Ta có phương trình:

(left( {12 – x} right){{4{rm{x}}} over 3} = 36 Leftrightarrow {x^2} – 12{rm{x}} + 27 = 0)

Giải phương trình ta được:

({x_1} = 9) (nhận) hoặc ({x_2} = 3) (nhận)

Vậy độ dài của đoạn (AK = 3cm) hoặc (9cm). Khi đó (M) sẽ có hai vị trí trên (AB) nhưng diện tích hình chữ nhật (MNPQ) luôn bằng (36) cm²

Trường

Giải bài tập