Giải bài tập trang 20 bài 4 Số trung bình cộng Sách giáo khoa (SGK) Toán 7. Câu 14: Hãy tính số trung bình cộng của dấu hiệu ở bài tập 9…
Bài 14 trang 20 sgk toán 7 – tập 2
Hãy tính số trung bình cộng của dấu hiệu ở bài tập 9.
Hướng dẫn giải:
Bạn đang xem: Giải bài 14, 15, 16 trang 20 SGK Toán 7
Bảng “tần số” ở bài tập 9 viết theo cột:
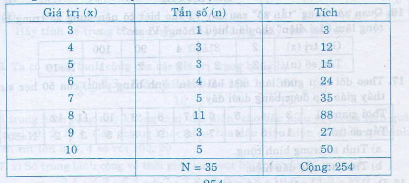
Vậy số trung bình cộng (overline{X}) là: (overline{X}) = (frac{254}{35}) ≈ 7,26.
Bài 15 trang 20 sgk toán 7 – tập 2
Nghiên cứu “tuổi thọ” của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. “Tuổi thọ” của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục) :

a) Dấu hiệu cần tìm hiểu ở đây là gì và số các giá trị là bao nhiêu ?
b) Tính số trung bình cộng.
c) Tìm mốt của dấu hiệu.
Hướng dẫn giải:
a) + Dấu hiệu: Thời gian cháy sáng liên tục cho tới lúc tự tắt của bóng đèn tức “tuổi thọ” của một loại bóng đèn.
+ Số các giá trị: N = 50
Số trung bình cộng của tuổi thọ các bóng đèn đó là:
(overline{X}=frac{1150.5 +1160.8+1170.12+1180.18+1190.7}{50})
(overline{X}) = 1172,8 (giờ)
c) Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay M0 = 1180.
Bài 16 trang 20 sgk toán 7 – tập 2
Quan sát bảng “tần số” (bảng 24) và cho biết có nên dùng số trung bình cộng làm “đại diện” cho dấu hiệu không ? Vì sao ?

Hướng dẫn giải:
Ta có số trung bình cộng của các giá trị trong bảng là:
(overline{X}=frac{2.3+3.2+4.2+90.2+100.1}{10}=frac{300}{10}=30)
Số trung bình cộng này không làm “đại diện” cho dấu hiệu vì chênh lệch quá lớn so với 2; 3; 4. Các giá trị khác nhau của dấu hiệu có khoảng chênh lệch rất lớn 2, 3, 4 so với 100, 90.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





