Giải bài tập trang 12, 13 bài 3 Phương trình đưa được về dạng ax + b = 0 sgk toán 8 tập 2. Câu 10: Tìm chỗ sai và sửa lại các bài giải sau cho đúng:…
Bài 10 trang 12 sgk toán 8 tập 2
Tìm chỗ sai và sửa lại các bài giải sau cho đúng:
a) 3x – 6 + x = 9 – x b) 2t – 3 + 5t = 4t + 12
Bạn đang xem: Giải bài 10, 11, 12, 13, 14, 15 trang 12, 13 SGK toán 8 tập 2
3x + x – x = 9 – 6 2t + 5t – 4t = 12 -3
3x = 3 3t = 9
x = 1 t = 3.
Hướng dẫn giải:
a) Sai ở phương trình thứ hai chuyển vế hạng tử -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu.
Giải lại: 3x – 6 + x = 9 – x
3x + x + x = 9 + 6
5x = 15
x = 3
Vậy phương trình có nghiệm duy nhất x = 3
b) Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại: 2t – 3 + 5t = 4t + 12
2t + 5t – 4t = 12 + 3
3t = 15
t = 5
Vậy phương trình có nghiệm duy nhất t = 5
Bài 11 trang 13 sgk toán 8 tập 2
Giải các phương trình:
a) 3x – 2 = 2x – 3; b) 3 – 4u + 24 + 6u = u + 27 + 3u;
c) 5 – (x – 6) = 4(3 – 2x); d) -6(1,5 – 2x) = 3(-15 + 2x);
e) 0,1 – 2(0,5t – 0,1) = 2(t – 2,5) – 0,7; f) ( frac{3}{2}(x -frac{5}{4})-frac{5}{8}) = x
Hướng dẫn giải:
a) 3x – 2 = 2x – 3
⇔ 3x – 2x = -3 + 2
⇔ x = -1
Vậy phương trình có nghiệm duy nhất x = -1.
b) 3 – 4u + 24 + 6u = u + 27 + 3u
⇔ 2u + 27 = 4u + 27
⇔ 2u – 4u = 27 – 27
⇔ -2u = 0
⇔ u = 0
Vậy phương trình có nghiệm duy nhất u = 0.
c) 5 – (x – 6) = 4(3 – 2x)
⇔ 5 – x + 6 = 12 – 8x
⇔ -x + 11 = 12 – 8x
⇔ -x + 8x = 12 – 11
⇔ 7x = 1
⇔ x = ( frac{1}{7})
Vậy phương trình có nghiệm duy nhất x = ( frac{1}{7}).
d) -6(1,5 – 2x) = 3(-15 + 2x)
⇔ -9 + 12x = -45 + 6x
⇔ 12x – 6x = -45 + 9
⇔ 6x = -36
⇔ x = -6
Vậy phương trình có nghiệm duy nhất x = -6
e) 0,1 – 2(0,5t – 0,1) = 2(t – 2,5) – 0,7
⇔ 0,1 – t + 0,2 = 2t – 5 – 0,7
⇔ -t + 0,3 = 2t – 5,7
⇔ -t – 2t = -5,7 – 0,3
⇔ -3t = -6
⇔ t = 2
Vậy phương trình có nghiệm duy nhất t = 2
f) ( frac{3}{2}(x -frac{5}{4})-frac{5}{8}) = x
⇔ ( frac{3}{2})x – ( frac{15}{8}) – ( frac{5}{8}) = x
⇔ ( frac{3}{2})x – x = ( frac{15}{8}) + ( frac{5}{8})
⇔ ( frac{1}{2})x = ( frac{20}{8})
⇔ x = ( frac{20}{8}) : ( frac{1}{2})
⇔ x = 5
Vậy phương trình có nghiệm duy nhất x = 5
Bài 12 trang 13 sgk toán 8 tập 2
Giải các phương trình:
a) ( frac{5x-2}{3}=frac{5-3x}{2}); b) ( frac{10x+3}{12}=1+frac{6+8x}{9})
c) ( frac{7x-1}{6}) + 2x = ( frac{16 – x}{5}); d)4(0,5 – 1,5x) = ( -frac{5x-6}{3})
Hướng dẫn giải:
a) ( frac{5x-2}{3}=frac{5-3x}{2}) ⇔ 2(5x – 2) = 3(5 – 3x)
⇔ 10x – 4 = 15 – 9x
⇔ 10x + 9x = 15 + 4
⇔ 19x = 19
⇔ x = 1
b) ( frac{10x+3}{12}=1+frac{6+8x}{9}) ⇔ ( frac{3(10x+3)}{36}=frac{36+4(6+8x)}{36})
⇔ 30x + 9 = 36 + 24 + 32x
⇔ 30x – 32x = 60 – 9
⇔ -2x = 51
⇔ x = ( frac{-51}{2}) = -25,5
Vậy phương trình có nghiệm duy nhất x = -25,5.
c) ( frac{7x-1}{6}) + 2x = ( frac{16 – x}{5}) ⇔ 7x -1 + 12x = 3(16 – x)
⇔ 7x -1 + 12x = 48 – 3x
⇔ 19x + 3x = 48 + 1
⇔ 22x = 49
⇔ x = ( frac{49}{22})
Vậy phương trình có nghiệm duy nhất x = ( frac{49}{22})
d) 4(0,5 – 1,5x) = ( -frac{5x-6}{3}) ⇔ 2 – 6x = ( -frac{5x-6}{3})
⇔ 6 – 18x = -5x + 6
⇔ -18x + 5x = 0
⇔ -13x = 0
⇔ x = 0
Vậy phương trình có nghiệm duy nhất x = 0.
Bài 13 trang 13 sgk toán 8 tập 2
Bạn Hoà giải phương trình x(x + 2) = x(x + 3) như hình 2.
Theo em bạn Hoà giải đúng hay sai?
Em sẽ giải phương trình đó như thế nào?
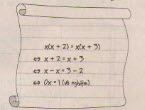
Hướng dẫn giải:
Bạn Hoà đã giải sai.
Không thể chia hai vế của phương trình đã cho với x để được phương trình
x + 2 = x + 3.
Lời giải đúng: x(x + 2) = x(x + 3)
⇔ x2 + 2x = x2 + 3x
⇔ x2 + 2x – x2 – 3x = 0
⇔ -x = 0
⇔ x = 0
Vậy phương trìnhđã cho có nghiệm là x = 0
Bài 14 trang 13 sgk toán 8 tập 2
Số nào trong ba số -1; 2 và -3 nghiệm đúng mỗi phương trình sau:
|x| = x (1), ({x^2} + 5x + 6 = 0left( 2 right)) , ({6 over {1 – x}} = x + 4left( 3 right))
Hướng dẫn làm bài:
Trong ba số -1, 2 và -3 thì
+) x = 2 nghiệm đúng phương trình |x| = x vì |2| = 2 (đúng).
+) x = -3 nghiệm đúng phương trình ({6 over {1 – x}} = x + 4left( 3 right))
Vì ({left( { – 3} right)^2} + 5.left( { – 3} right) + 6 = 0)
(9 – 15 + 6 = 0)
0 = 0
+) (x = – 1) nghiệm đúng phương trình ({6 over {1 – x}} = x + 4) vì:
({6 over {1 – left( { – 1} right)}} = – 1 + 4 Leftrightarrow {6 over 2} = 3 Leftrightarrow 3 = 3)
Bài 15 trang 13 sgk toán 8 tập 2
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32 km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48 km/h. Hãy viết phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành.
Hướng dẫn làm bài:
Gọi x là thời gian chuyển động của ô tô (x > 0; giờ)
Đoạn đường của ô tô đi trong x giờ: 48 x
Đoạn đường của xe máy đi trong x giờ: 32x
Vì xe máy khởi hành trước ô tô là 1 giờ nên khi hai xe cùng khởi hành thì đã cách nhau 32 km.
Ta có phương trình cần tìm:
48x – 32 x = 32
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





