Giải bài tập trang 84 bài 4 đường trung bình của tam giác, của hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 34: Chứng minh rằng AI = IM…
Câu 34 trang 84 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC, điểm D thuộc cạnh AC sao cho (AD = {1 over 2}DC). Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.
Giải:
Bạn đang xem: Giải bài 34, 35, 36 trang 84 SBT Toán 8 tập 1
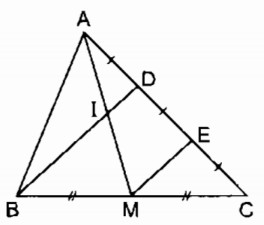
Gọi E là trung điểm của DC
Trong ∆ BDC ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ ME // BD( tính chất đường trung bình của tam giác)
Suy ra: DI // ME
(AD = {1 over 2}DC) (gt)
(DE = {1 over 2}DC) (theo cách vẽ)
⇒AD = DE
DI // ME
Nên AI = IM (tính chất đường trung bình của tam giác)
Câu 35 trang 84 Sách bài tập (SBT) Toán 8 tập 1
Hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, I, F thẳng hàng.
Giải:

Hình thang ABCD có AB// CD
E là trung điểm của AD (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của hình thang ABCD
⇒ EF // CD (tính chất đường trung bình hình thang) (1)
Trong ∆ ADC có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ADC
⇒ EI // CD (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) theo tiên đề Ơclít đường thẳng EF và EI trùng nhau
Vậy E, I, F thẳng hàng.
Câu 36 trang 84 Sách bài tập (SBT) Toán 8 tập 1
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a. EI// CD, IF // AB
b. (EF le {{AB + CD} over 2})
Giải:

a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và (EI = {{CD} over 2})
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và (IF = {{AB} over 2})
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà (EI = {{CD} over 2}{rm{;}},,IF{rm{ = }}{{AB} over 2}) (chứng minh trên) ( Rightarrow {rm{EF}} le {{CD} over 2} + {{AB} over 2})
Vậy (EF le {{AB + CD} over 2}) (dấu bằng xảy ra khi AB // CD)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





