Giải bài tập trang 122, 123 bài 3 Diện tích tam giác sgk toán lớp 8 tập 1. Câu 21: Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE (h.134)…
Bài 21 trang 122 sgk toán lớp 8 tập 1
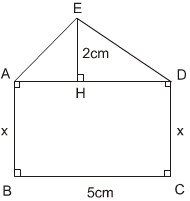
Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE (h.134)
Bạn đang xem: Giải bài 21, 22, 23, 24, 25 trang 122, 123 SGK toán lớp 8 tập 1
Hướng dẫn giải:
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm
Bài 22 trang 122 sgk toán lớp 8 tập 1
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135).

Hãy chỉ ra:
a) Một điểm I sao cho SPIF = SPAF
b) Một điểm O sao cho SPOF = 2. SPAF
c) Một điểm N sao cho SPNF =  SPAF
SPAF
Hướng dẫn giải:
Từ hình trên đề bài ta có
a) Nếu lấy điểm I bất kì nằm trên đường thẳng d đi qua A và song song với đường thẳng PF thì SPIF = SPAF
b) Nếu lấy một điểm O sao cho khoảng cách từ O đến đường thẳng PF bằng hai lần khoảng cách từ A đến đường thẳng PF thì SPOF = 2. SPAF
Có vô số điểm O như thế.
c) Nếu lấy điểm N sao cho khoảng cách từ N đến đường thẳng PF bằng  khoảng cách từ A đến PF thì SPNF =
khoảng cách từ A đến PF thì SPNF =  SPAF.
SPAF.
Có vô số điểm như thế nằm trên hai dường thẳng song song với đường thẳng PF
Bài 23 trang 123 sgk toán lớp 8 tập 1
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho:
SMAC = SAMB + SBMC
Hướng dẫn giải:

Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho SMAC = SAMB + SBMC
Nhưng SAMB + SBMC + SMAC = SABC
Suy ra SMAC = SABC
∆ MAC = ∆ABC có chung đáy BC nên MK =  BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
Bài 24 trang 123 sgk toán lớp 8 tập 1
Tính diện tích tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
Hướng dẫn giải:
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.

Theo định lý Pitago ta có
h2 = b2 – ![]() =
= ![]()
h = ![]()
Nên S =  ah =
ah =  a.
a. ![]() =
=  a.
a. 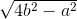 .
.
Bài 25 trang 123 sgk toán lớp 8 tập 1
Tính diện tích của một tam giác đều có cạnh là a.
Hướng dẫn giải:
Gọi h là chiều cao của tam giác đều cạnh a
Theo định lí Pitago ta có:
({h^2} = {a^2} – {left( {{a over 2}} right)^2} = {{3{{rm{a}}^2}} over 4})
Nên (h = {{asqrt 3 } over 2})
Vậy (S = {1 over 2}ah = {1 over 2}a.{{asqrt 3 } over 2} = {{{a^2}sqrt 3 } over 4})
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





