Giải bài tập trang 82 bài 2 hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 18: Cho tam giác AbC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B…
Câu 18 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác AbC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì ? Vì sao ?
Giải:
Bạn đang xem: Giải bài 18, 19, 20 trang 82 SBT Toán 8 tập 1
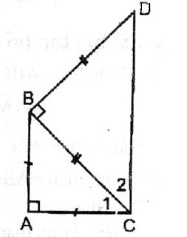
Vì ∆ ABC vuông cân tại A nên ({widehat C_1} = {45^0})
Vì ∆ BCD vuông cân tại B nên ({widehat C_2} = {45^0})
(widehat {ACD} = {widehat C_1} + {widehat C_2} = {45^0} + {45^0} = {90^0})
⇒ AC ⊥ CD
AC ⊥ AB (gt)
Suy ra: AB // CD. Vậy tứ giác ABDC là hình thang vuông.
Câu 19 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Hình thang vuông ABCD có , AB=AD=2cm, DC= 4cm. Tính các góc của hình thang.
Giải:

Kẻ BH ⊥ CD
Ta có: AD ⊥ CD (gt)
Suy ra: BH // AD.
Hình thang ABHD có hai cạnh bên song song
Nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD =4− 2=2cm
Suy ra: ∆ BHC vuông cân tại H
(widehat B + widehat C = {180^0}) (hai góc trong cùng phía)
(Rightarrow widehat B = {180^0} – widehat C = {180^0} – {45^0} = {135^0})
Câu 20 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy.
Giải:

Giả sử hình thang ABCD có AB // CD và CD > AB
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song
Nên AB = ED và AD = BE
Ta có: CD− AB =CD – ED =EC (1)
Trong ∆ BEC ta có:
BE + BC > EC ( bất đẳng thức tam giác)
Mà BE = AD
Suy ra: AD+ BC > EC (2)
Từ (1) và (2) suy ra: AD+BC > CD – AB
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





