Giải bài tập trang 60, 61 bài 1 nhắc lại và bổ sung các khái niệm về hàm số Sách bài tập (SBT) Toán 9 tập 1. Câu 4: Chứng minh rằng hàm số đồng biến trên R….
Câu 4 trang 60 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hàm số (y = fleft( x right) = {2 over 3}x + 5) với $x in R$
Chứng minh rằng hàm số đồng biến trên R.
Bạn đang xem: Giải bài 4, 5 trang 60, 61 SBT Toán 9 tập 1
Gợi ý làm bài:
Xét hàm số (y = fleft( x right) = {2 over 3}x + 5)
Với hai số (x_1) và (x_2) thuộc R, ta có:
({{rm{y}}_1} = fleft( {{x_1}} right) = {2 over 3}{x_1} + 5)
({{rm{y}}_2} = fleft( {{x_2}} right) = {2 over 3}{x_2} + 5)
Nếu ({x_1} 0)
Khi đó:
(fleft( {{x_2}} right) – fleft( {{x_1}} right))
(= left( {{2 over 3}{x_2} + 5} right) – left( {{2 over 3}{x_1} + 5} right) = {2 over 3}left( {{x_2} – {x_1}} right) > 0)
Suy ra: (fleft( {{x_2}} right) > fleft( {{x_1}} right))
Vậy hàm số đồng biến trên R.
Câu 5 trang 61 Sách Bài Tập (SBT) Toán 9 Tập 1
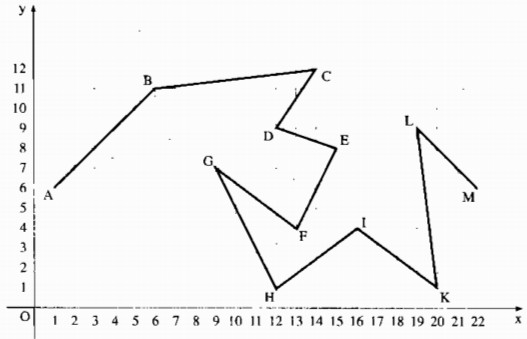
Biểu diễn các điểm sau đây trên cùng một hệ trục tọa độ. Nối theo thứ tự các điểm đã cho bằng các đoạn thẳng để được một đường gấp khúc với điểm đầu là điểm A, điểm cuối là M.
|
A(1; 6) |
B(6; 11) |
C(14; 12) |
D(12; 9) |
|
E(15; 8) |
F(13; 4) |
G(9; 7) |
H(12; 1) |
|
I(16; 4) |
K(20; 1) |
L(19; 9) |
M(22; 6) |
Gợi ý làm bài:
Dựng hệ trục tọa độ Oxy, rồi dựng các điểm theo tọa độ của chúng, nối theo thứ tự các điểm , ta được một đường gấp khúc như hình dưới:
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





