Giải bài tập trang 27, 28 bài 4 quy đồng mẫu thức nhiều phân thức Sách bài tập (SBT) Toán 8 tập 1. Câu 13: Quy đồng mẫu thức các phân thức…
Câu 13 trang 27 Sách bài tập (SBT) Toán 8 tập 1
Quy đồng mẫu thức các phân thức:
a. ({{25} over {14{x^2}y}},{{14} over {21x{y^5}}})
Bạn đang xem: Giải bài 13, 14, 15, 16 trang 27, 28 SBT Toán 8 tập 1
b. ({{11} over {102{x^4}y}},{3 over {34x{y^3}}})
c. ({{3x + 1} over {12x{y^4}}},{{y – 2} over {9{x^2}{y^3}}})
d. ({1 over {6{x^3}{y^2}}},{{x + 1} over {9{x^2}{y^4}}},{{x – 1} over {4x{y^3}}})
e. ({{3 + 2x} over {10{x^4}y}},{5 over {8{x^2}{y^2}}},{2 over {3x{y^5}}})
f. ({{4x – 4} over {2xleft( {x + 3} right)}},{{x – 3} over {3xleft( {x + 1} right)}})
g. ({{2x} over {{{left( {x + 2} right)}^3}}},{{x – 2} over {2x{{left( {x + 2} right)}^2}}})
h. ({5 over {3{x^3} – 12x}},{3 over {left( {2x + 4} right)left( {x + 3} right)}})
Giải:
a. MTC ( = 42{x^2}{y^5})
({{14} over {21x{y^5}}} = {2 over {3x{y^5}}})( = {{2.14x} over {3x{y^5}.14x}} = {{28x} over {42{x^2}{y^5}}}); ({{25} over {14{x^2}y}} = {{25.{3y^4}} over {14{x^2}y.{3y^4}}} = {{75{y^4}} over {42{x^2}{y^5}}})
b. MTC = (102{x^4}{y^3})
({{11} over {102{x^4}y}} = {{11.{y^2}} over {102{x^4}y.{y^2}}} = {{11{y^2}} over {102{x^4}{y^3}}}); ({3 over {34x{y^3}}} = {{3.3{x^3}} over {34x{y^3}.3{x^3}}} = {{9{x^3}} over {102{x^4}{y^3}}})
c. MTC = (36{x^2}{y^4})
({{3x + 1} over {12x{y^4}}} = {{left( {3x + 1} right).3x} over {12x{y^4}.3x}} = {{9{x^2} + 3x} over {36{x^2}{y^4}}}); ({{y – 2} over {9{x^2}{y^3}}} = {{left( {y – 2} right).4y} over {9{x^2}{y^3}.4y}} = {{4{y^2} – 8y} over {36{x^2}{y^4}}})
d. MTC = (36{x^3}{y^4})
({1 over {6{x^3}{y^2}}} = {{1.6{y^2}} over {6{x^3}{y^2}.6{y^2}}} = {{6{y^2}} over {36{x^3}{y^4}}}); ({{x + 1} over {9{x^2}{y^4}}} = {{left( {x + 1} right).4x} over {9{x^2}{y^4}.4x}} = {{4{x^2} + 4x} over {36{x^3}{y^4}}})
({{x – 1} over {4x{y^3}}} = {{left( {x – 1} right).9{x^2}y} over {4x{y^3}.9{x^2}y}} = {{9{x^3}y – 9{x^2}y} over {36{x^3}{y^4}}})
e. MTC = (120{x^4}{y^5})
({{3 + 2x} over {10{x^4}y}} = {{left( {3 + 2x} right).12{y^4}} over {10{x^4}y.12{y^4}}} = {{36{y^4} + 24x{y^4}} over {120{x^4}{y^5}}})
({5 over {8{x^2}{y^2}}} = {{5.15{x^2}{y^3}} over {8{x^2}{y^2}.15{x^2}{y^3}}} = {{75{x^2}{y^3}} over {120{x^4}{y^5}}})
({2 over {3x{y^5}}} = {{2.40{x^3}} over {3x{y^5}.40{x^3}}} = {{80{x^3}} over {120{x^4}{y^5}}})
f. MTC = (3xleft( {x + 3} right)left( {x + 1} right)) Vì ({{4x – 4} over {2xleft( {x + 3} right)}} = {{2left( {x – 1} right)} over {xleft( {x + 3} right)}})
({{4x – 4} over {2xleft( {x + 3} right)}} = {{2left( {x – 1} right)} over {xleft( {x + 3} right)}} = {{2left( {x – 1} right).3left( {x + 1} right)} over {xleft( {x + 3} right).3left( {x + 1} right)}} = {{6left( {{x^2} – 1} right)} over {3xleft( {x + 3} right)left( {x + 1} right)}})
({{x – 3} over {3xleft( {x + 1} right)}} = {{left( {x – 3} right)left( {x + 3} right)} over {3xleft( {x + 1} right)left( {x + 3} right)}} = {{{x^2} – 9} over {3xleft( {x + 1} right)left( {x + 3} right)}})
g. MTC = (2x{left( {x + 2} right)^3})
({{2x} over {{{left( {x + 2} right)}^3}}} = {{2x.2x} over {2x{{left( {x + 2} right)}^3}}} = {{4{x^2}} over {2x{{left( {x + 2} right)}^3}}})
({{x – 2} over {2x{{left( {x + 2} right)}^2}}} = {{left( {x – 2} right)left( {x + 2} right)} over {2x{{left( {x + 2} right)}^2}left( {x + 2} right)}} = {{{x^2} – 4} over {2x{{left( {x + 2} right)}^3}}})
h. (3{x^3} – 12x = 3xleft( {{x^2} – 4} right) = 3xleft( {x – 2} right)left( {x + 2} right))
(left( {2x + 4} right)left( {x + 3} right) = 2left( {x + 2} right)left( {x + 3} right))
MTC = (6xleft( {x – 2} right)left( {x + 2} right)left( {x + 3} right))
(eqalign{ & {5 over {3{x^3} – 12x}} = {5 over {3xleft( {x – 2} right)left( {x + 2} right)}} = {{5.2left( {x + 3} right)} over {3xleft( {x – 2} right)left( {x + 2} right).2left( {x + 3} right)}} cr & = {{10left( {x + 3} right)} over {6xleft( {x – 2} right)left( {x + 2} right)left( {x + 3} right)}} cr & {3 over {left( {2x + 4} right)left( {x + 3} right)}} = {3 over {2left( {x + 2} right)left( {x + 3} right)}} = {{3.3xleft( {x – 2} right)} over {2left( {x + 2} right)left( {x + 3} right).3xleft( {x – 2} right)}} cr & = {{9xleft( {x – 2} right)} over {6xleft( {x + 2} right)left( {x – 2} right)left( {x + 3} right)}} cr} )
Câu 14 trang 27 Sách bài tập (SBT) Toán 8 tập 1
Quy đồng mẫu thức các phân thức:
a. ({{7x – 1} over {2{x^2} + 6x}},{{5 – 3x} over {{x^2} – 9}})
b. ({{x + 1} over {x – {x^2}}},{{x + 2} over {2 – 4x + 2{x^2}}})
c. ({{4{x^2} – 3x + 5} over {{x^3} – 1}},{{2x} over {{x^2} + x + 1}},{6 over {x – 1}})
d. ({7 over {5x}},{4 over {x – 2y}},{{x – y} over {8{y^2} – 2{x^2}}})
e. ({{5{x^2}} over {{x^3} + 6{x^2} + 12x + 8}},{{4x} over {{x^2} + 4x + 4}},{3 over {2x + 4}})
Giải:
a. (2{x^2} + 6x = 2xleft( {x + 3} right);{x^2} – 9 = left( {x + 3} right)left( {x – 3} right)) MTC = (2xleft( {x + 3} right)left( {x – 3} right))
(eqalign{ & {{7x – 1} over {2{x^2} + 6x}} = {{7x – 1} over {2xleft( {x + 3} right)}} = {{left( {7x – 1} right)left( {x – 3} right)} over {2xleft( {x + 3} right)left( {x – 3} right)}} cr & {{5 – 3x} over {{x^2} – 9}} = {{5 – 3x} over {left( {x + 3} right)left( {x – 3} right)}} = {{2xleft( {5 – 3x} right)} over {2xleft( {x + 3} right)left( {x – 3} right)}} cr} )
b. (x – {x^2} = xleft( {1 – x} right)); (2 – 4x + 2{x^2} = 2left( {1 – 2x + {x^2}} right) = 2{left( {1 – x} right)^2})
MTC = (2x{left( {1 – x} right)^2})
(eqalign{ & {{x + 1} over {x – {x^2}}} = {{x + 1} over {xleft( {1 – x} right)}} = {{left( {x + 1} right).2left( {1 – x} right)} over {xleft( {1 – x} right).2left( {1 – x} right)}} = {{2{{left( {1 – x} right)}^2}} over {2x{{left( {1 – x} right)}^2}}} cr & {{x + 2} over {2 – 4x + 2{x^2}}} = {{x + 2} over {2{{left( {1 – x} right)}^2}}} = {{left( {x + 2} right).x} over {2x{{left( {1 – x} right)}^2}}} cr} )
c. ({x^3} – 1 = left( {x – 1} right)left( {{x^2} + x + 1} right)) MTC = ({x^3} – 1) ({{4{x^2} – 3x + 5} over {{x^3} – 1}});
(eqalign{ & {{2x} over {{x^2} + x + 1}} = {{2xleft( {x + 1} right)} over {left( {{x^2} + x + 1} right)left( {x – 1} right)}} = {{2xleft( {x – 1} right)} over {{x^3} – 1}} cr & {6 over {x – 1}} = {{6left( {{x^2} + x + 1} right)} over {left( {x – 1} right)left( {{x^2} + x + 1} right)}} = {{6left( {{x^2} + x + 1} right)} over {{x^3} – 1}} cr} )
d. (8{y^2} – 2{x^2} = 2left( {4{y^2} – {x^2}} right) = 2left( {2y + x} right)left( {2y – x} right))
MTC = (10xleft( {2y + x} right)left( {2y – x} right))
(eqalign{ & {7 over {5x}} = {{7.2left( {2y + x} right)left( {2y – x} right)} over {5x.2left( {2y + x} right)left( {2y – x} right)}} = {{14left( {2y + x} right)left( {2y – x} right)} over {10xleft( {2y + x} right)left( {2y – x} right)}} cr & {4 over {x – 2y}} = {{ – 4} over {2y – x}} = {{ – 4.10xleft( {2y + x} right)} over {left( {2y – x} right).10xleft( {2y + x} right)}} = {{ – 40xleft( {2y + x} right)} over {10xleft( {2y + x} right)left( {2y – x} right)}} cr & {{x – y} over {8{y^2} – 2{x^2}}} = {{x – y} over {2left( {2y + x} right)left( {2y – x} right)}} = {{left( {x – y} right).5x} over {2left( {2y + x} right)left( {2y – x} right).5x}} cr & = {{5xleft( {x – y} right)} over {10xleft( {2y + x} right)left( {2y – x} right)}} cr} )
e. (eqalign{ & {x^3} + 6{x^2} + 12x + 8 = {x^3} + 3{x^2}.2 + 3.x{.2^2} + {2^3} = {left( {x + 2} right)^3} cr & {x^2} + 4x + 4 = {left( {x + 2} right)^2};2x + 4 = 2left( {x + 2} right) cr} )
MTC =(2{left( {x + 2} right)^3})
(eqalign{ & {{5{x^2}} over {{x^3} + 6{x^2} + 12x + 8}} = {{5{x^2}} over {{{left( {x + 2} right)}^3}}} = {{5{x^2}.2} over {{{left( {x + 2} right)}^3}.2}} = {{10{x^2}} over {2{{left( {x + 2} right)}^3}}} cr & {{4x} over {{x^2} + 4x + 4}} = {{4x} over {{{left( {x + 2} right)}^2}}} = {{4x.2left( {x + 2} right)} over {{{left( {x + 2} right)}^2}.2left( {x + 2} right)}} = {{8xleft( {x + 2} right)} over {2{{left( {x + 2} right)}^3}}} cr & {3 over {2x + 4}} = {3 over {2left( {x + 2} right)}} = {{3{{left( {x + 2} right)}^2}} over {2left( {x + 2} right){{left( {x + 2} right)}^2}}} = {{3{{left( {x + 2} right)}^2}} over {2{{left( {x + 2} right)}^3}}} cr} )
Câu 15 trang 28 Sách bài tập (SBT) Toán 8 tập 1
Cho đa thức B ( = 2{x^3} + 3{x^2} – 29x + 30) và hai phân thức
({x over {2{x^2} + 7x – 15}}), ({{x + 2} over {{x^2} + 3x – 10}})
a. Chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho.
b. Quy đồng mẫu thức của hai phân thức đã cho.
Giải:
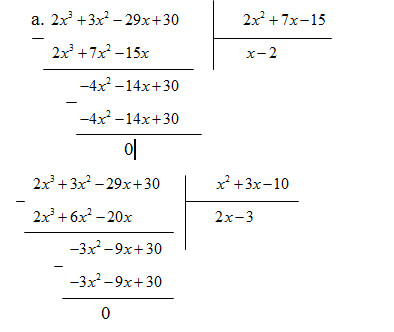
b. MTC = (2{x^3} + 3{x^2} – 29x + 30)
(eqalign{ & {x over {2{x^2} + 7x – 15}} = {{xleft( {x – 2} right)} over {left( {2{x^2} + 7x – 15} right)left( {x – 2} right)}} = {{{x^2} – 2x} over {2{x^3} + 3{x^2} – 29x + 30}} cr & {{x + 2} over {{x^2} + 3x – 10}} = {{left( {x + 2} right)left( {2x – 3} right)} over {left( {{x^2} + 3x – 10} right)left( {2x – 3} right)}} = {{left( {x + 2} right)left( {x – 3} right)} over {2{x^3} + 3{x^2} – 29x + 30}} cr} )
Câu 16 trang 28 Sách bài tập (SBT) Toán 8 tập 1
Cho hai phân thức ({1 over {{x^2} + 7x – 15}}) và ({2 over {{x^2} – 2x – 3}})
Chứng tỏ rằng có thể chọn đa thức ({x^3} – 7{x^2} + 7x + 15) làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức.
Giải:

Suy ra: ({x^3} – 7{x^2} + 7x + 15 = left( {{x^2} – 4x – 5} right)left( {x – 3} right))

Suy ra: ({x^3} – 7{x^2} + 7x + 15 = left( {{x^2} – 2x – 3} right)left( {x – 5} right))
(eqalign{ & {1 over {{x^2} – 4x – 5}} = {{1.left( {x – 3} right)} over {left( {{x^2} – 4x – 5} right).left( {x – 3} right)}} = {{x – 3} over {{x^3} – 7{x^2} + 7x + 15}} cr & {2 over {{x^2} – 2x – 3}} = {{2.left( {x – 5} right)} over {left( {{x^2} – 2x – 3} right)left( {x – 5} right)}} = {{2left( {x – 5} right)} over {{x^3} – 7{x^2} + 7x + 15}} cr} )
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





