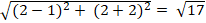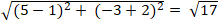Cách viết phương trình đường phân giác của góc cực hay
Việc viết phương trình đường phân giác của góc học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các em củng cố thêm phần kiến thức Toán học vô cùng quan trọng này, đã chia sẻ bài viết sau đây. Ở đây ngoài phần lý thuyết cần ghi nhớ, còn có thêm nhiều dạng bài tập, bạn có thể luyện thêm.
I. CÁCH VIẾT PHƯƠNG TRÌNH ĐƯỜNG PHÂN GIÁC CỦA GÓC
1. Phương pháp giải
Bạn đang xem: Cách viết phương trình đường phân giác của góc cực hay
Cho 2 đường thẳng cắt nhau: (d1) A1x + b1y + C1 = 0 và (d2): A2x + B2y + C2 = 0.
Phương trình các đường phân giác của góc tạo bởi 2 đường thẳng đó là:
![]()
Chú ý:
Cho đường thẳng ∆: Ax + By + C = 0 và hai điểm A(xA; yA); B(xB;yB ).
Đặt f(x;y) = Ax + By + C:
+ A và B nằm về cùng một phía đối với ∆ ⇔ f(xA; yA). f(xB; yB) > 0
+ A và B nằm khác phía đối với ∆ ⇔ f(xA; yA). f(xB; yB) < 0
2. Ví dụ minh họa
Ví dụ 1. Cho đường thẳng d: 3x + 4y – 5 = 0 và 2 điểm A( 1; 3) ; B( 2; m) . Tìm m để A và B nằm cùng phía đối với d?
A. m < 0 B. m > – 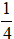
Hướng dẫn giải
Hai điểm A và B nằm về hai phía của đường thẳng d khi và chỉ khi:
( 3 + 12 – 5)( 6 + 4m – 5) < 0 hay m > –
Chọn B.
Ví dụ 2. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(0; 2) , B( 1; 2) và C(3; 6 ) . Phương trình đường phân giác trong của góc A là:
A. 2x + y – 2 = 0 B. x – 2y + 4 = 0 C. 2x + y – 4 = 0 D. Đáp án khác
Lời giải
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB : ![]()
⇒ ( AB) : 0(x – 0) + 1(y – 2) = 0 hay y – 2 = 0
Đường thẳng AC : ![]()
⇒ ( AC) : 4(x – 0) – 3(y – 2) = 0 hay 4x – 3y + 6 = 0
Suy ra các đường phân giác góc A là: ![]()
⇔ |4x – 3y + 6| = 5|y – 2|
![]()
Đặt f( x; y) = x – 2y + 4
⇒ f( B).f( C) =( 1 – 2.2 + 4) ( 3 – 2.6 + 4) = -5 < 0
⇒ B và C nằm khác phía so với đường thẳng : x – 2y + 4 = 0.
suy ra đường phân giác trong góc A là x – 2y + 4 = 0
Chọn B.
Ví dụ 3. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A( 1; 5) ; B( -4; -5) và C( 4; -1) . Phương trình đường phân giác ngoài của góc A là:
A. y + 5 = 0 B. y – 5 = 0 C. x + 1 = 0 D. x – 1 = 0
Lời giải
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB : ![]()
⇒ ( AB) : 2( x – 1) – 1.( y – 5) = 0 hay 2x – y + 3 = 0
Đường thẳng AC : ![]()
⇒ ( AC) : 2( x – 1) + 1( y – 5) = 0 hay 2x + y – 7 = 0
Suy ra các đường phân giác góc A là: ![]()
⇔ |2x – y + 3| = |2x + y – 7|
⇔ ![]()
Đặt f( x; y) = y – 5
⇒ f(B).f(C) = ( -5 – 5).( -1 – 5) = 60 > 0
⇒ B và C nằm cùng phía so với đường thẳng : y – 5 = 0.
suy ra đường phân giác ngoài góc A là y – 5 = 0
Chọn B.
Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: 3x – 4y – 3 = 0 và d2 : 12x + 5y – 12 = 0. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng d1 và d2 là:
A. 3x + 11y – 3 = 0 B. 11x – 3y – 11 = 0 C. 3x – 11y – 3 =0 D. 11x + 3y – 11 = 0
Lời giải
Các đường phân giác của các góc tạo bởi hai đường thẳng d1 và d2 là:
![]() ⇔ 13|3x – 4y – 3| = 5|12x + 5y – 12| .
⇔ 13|3x – 4y – 3| = 5|12x + 5y – 12| .
![]()
Gọi I là giao điểm của d1 và d2; tọa độ I là nghiệm hệ
![]() ⇒ I( 1;0)
⇒ I( 1;0)
+ Gọi đường thẳng d: 3x + 11y – 3 = 0. Lấy điểm M(-10; 3) thuộc đường thẳng d.
Gọi H là hình chiếu của M lên d1.
Ta có: IM = 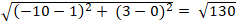
MH = d(M;d1 ) = ![]() = 9
= 9
Suy ra ![]()
Suy ra d: 3x + 11y – 3 = 0 là đường phân giác góc tù nên đường phân giác góc nhọn là 11x – 3y – 11 = 0.
Chọn B.
II. BÀI TẬP VỀ PHƯƠNG TRÌNH ĐƯỜNG PHÂN GIÁC
Bài 1. Cho hai đường thẳng d: x + 2y + 3 = 0 và d’: 2x + y + 3 = 0. Phương trình các đường phân giác của các góc tạo bởi d và d’ là:
A. x + y = 0 và x – y + 4 = 0 . B. x – y + 4 = 0 và x + y – 2 = 0 .
C. x + y + 2 = 0 và x – y = 0 D. x + y + 1 = 0 và x – y – 3 = 0 .
Hướng dẫn giải
Phương trình các đường phân giác của các góc tạo bởi d và d’ là:
![]()
Vậy phương trình các đường phân giác tạo bởi d và d’ là :
x – y = 0 và x + y + 2 = 0
Chọn C.
Bài 2. Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường thẳng ∆1: x + 2y – 3 = 0 và ∆2: 2x – y + 3 = 0.
A. x + 3y – 2 = 0 và x = 3y. B. 3x = – y và x – 3y – 6 = 0.
C. 3x + y = 0 và –x + 3y – 6 = 0. D. Đáp án khác
Hướng dẫn giải
Gọi M(x; y) là điểm thuộc đường phân giác tạo bởi 2 đường thẳng đã cho.
⇒ d(M,Δ1) = d(M,Δ2) ⇒ ![]()
⇒ x + 2y – 3 = ± (2x – y + 3) ⇒ ![]()
Chọn C.
Bài 3: Cho tam giác ABC có AB: 2x – y + 4 = 0; AC: x – 2y – 6 = 0 và hai điểm B; C thuộc Ox. Phương trình phân giác ngoài của góc BAC là
A. 3x – 3y – 2 = 0 B. x + y + 10 = 0 C. 3x + 3y + 2 = 0 D. x + y – 2 = 0
Hướng dẫn giải:
Do hai điểm B và C thuộc Ox nên tọa độ hai điểm đó là : B(-2; 0) và C(6; 0).
Gọi M( x; y) thuộc đường phân giác của góc BAC
Ta có: d(M, AB) = d(M, AC) ⇔ ![]() ⇔ |2x – y + 4| = |x – 2y – 6|
⇔ |2x – y + 4| = |x – 2y – 6|
⇔ 
+ Xét vị trí của hai điểm B và C đối với đường thẳng x + y + 10 = 0.
Ta có : (-2 + 0 + 10).( 6 + 0 + 10) > 0 nên hai điểm B và C nằm cùng phía so với đường thẳng x + y + 10 = 0.
Suy ra đường thẳng x + y + 10 = 0 là đường phân giác ngoài của góc BAC.
Chọn B.
Bài 5: Cho hai đường thẳng d : x + 2y + 3 = 0 và d’ : 2x + y + 3 = 0. Phương trình các đường phân giác của các góc tạo bởi d và d’ là
A. x + y = 0 ; x – y + 2 = 0 B. x – y = 0 ; x + y + 2 = 0
C. x + y + 2 = 0 ; x – y = 0 D. x + y – 2 = 0 ; x – y – 1 = 0
Đáp án: C
Trả lời:
Ta có: M(x ; y) thuộc đường phân giác khi và chỉ khi :
d(M; d) = d(M; d’) ⇔ ![]()
⇔ |x + 2y + 3| = |2x + y + 3| ⇔ 
Bài 6: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng
∆: x + y = 0 và trục hoành Ox.
A. (1 + √2)x + y = 0 ; x – (1 – √2)y = 0 . B. (1 + √2)x + y = 0; x + (1 – √2)y = 0 .
C. (1 + √2)x – y = 0; x + (1 – √2)y = 0 . D. Tất cả sai
Đáp án: D
Trả lời:
Gọi M(x; y) là điểm thuộc đường phân giác
Theo đầu bài ta có: d( M; ∆) = d( M; Ox)
⇒ ![]() ⇔ |x + y| = √2|y|
⇔ |x + y| = √2|y|
⇔![]()
Bài 7: Cho tam giác ABC có A(-2; -1); B(-1; 3) và C( 6; 1).Viết phương trình đường phân giác ngoài góc A của tam giác ABC.
A. x – y + 1 = 0 B. 5x + 3y + 9 = 0 C. 3x + 3y – 5 = 0 D. x + y + 3 = 0
Đáp án: D
Trả lời:
+ Phương trình đường thẳng AB: ![]()
⇒ Phương trình AB: 4( x + 2) – 1( y + 1) = 0 hay 4x – y + 7 = 0
+ Phương trình đường thẳng AC: ![]()
⇒ Phương trình AC: 1( x + 2) – 4( y + 1) = 0 hay x – 4y – 2 = 0
+ Phương trình các đường phân giác góc A là:

Đặt f1( x; y) = x + y + 3 ta có: f1(B).f1(C) > 0
Suy ra B và C nằm cùng phía so với d1 và khác phía so với d2.
Vậy phương trình đường phân giác ngoài góc A là: x + y + 3 = 0.
Bài 8: Cho tam giác ABC có phương trình các cạnh AB: x + y – 1 = 0;
AC: 7x – y + 2 = 0 và BC: 10x + y – 19 = 0. Viết phương trình đường phân giác trong góc A của tam giác ABC.
A. 12x + 4y – 3 = 0 B. 2x + 6y + 7 = 0 C. 12x + 6y – 7 = 0 D. 2x – 6y +7 = 0
Đáp án: D
Trả lời:
+ AB và BC giao nhau tại B nên tọa độ của B là nghiệm hệ :
![]() ⇒ B( 2; -1)
⇒ B( 2; -1)
+ AC và BC cắt nhau tại C nên tọa độ C là nghiệm hệ:
![]() ⇒ C(1; 9)
⇒ C(1; 9)
+ Phương trình các đường phân giác góc A là:

Đặt f1( x; y) = 2x – 6y + 7 ta có f1(B) . f1( C) < 0
Suy ra B và C nằm khác phía so với d1 và cùng phía so với d2.
Vậy phương trình đường phân giác trong góc A là: 2x – 6y + 7 = 0
Bài 9: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; -1) ; B( -1;3) và C( 4; -1) . Phương trình đường phân giác ngoài của góc A là:
A. y + 5 = 0 B. x + 2y = 0 C. x + 1 = 0 D. 2x – y – 5 = 0
Đáp án: B
Trả lời:
+ Ta viết phương trình đường thẳng AB và AC:
Đường thẳng AB : ![]()
⇒ ( AB) : 4(x – 2) + 3( y + 1) = 0 hay 4x + 3y – 5 = 0
Đường thẳng AC : ![]()
⇒ ( AC) : 0(x – 2) + 1( y + 1) = 0 hay y + 1 = 0
Suy ra các đường phân giác góc A là: ![]()
⇔ |4x + 3y – 5| = 5|y + 1|
⇔ ![]()
Đặt f( x; y) = 2x – y – 5
⇒ f( B).f( C) = (- 2 – 3 – 5).( 2.4 + 1 – 5) = -40 < 0
⇒ B và C nằm khác phía so với đường thẳng 2x – y – 5 = 0
suy ra đường phân giác ngoài góc A là x + 2y = 0
Bài 10: Cho tam giác ABC có A(1; -2); B( 2; 2) và C(5; -3). Viết phương trình đường phân giác trong xuất phát từ đỉnh A của tam giác ABC?
A. 5x + 3y + 1 = 0 B. 3x + 2y + 1 = 0 C. x + y + 1 = 0 D. 5x + 2y – 1 = 0
Đáp án: A
Trả lời:
+Ta có: AB =
AC =
⇒ AB = AC nên tam giác ABC cân tại A.
⇒ Đường phân giác trong xuất phát từ A đồng thời là đường trung tuyến.
+ Gọi M là trung điểm BC; tọa độ M :

+ Đường thẳng AM: 
⇒ Phương trình AM: 5( x – 1) + 3( y + 2) = 0 hay 5x + 3y + 1 = 0
Trên đây đã giới thiệu đến các bạn cách viết phương trình đường phân giác của góc và nhiều dạng bài tập thường gặp. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Xem thêm cách tìm Vectơ chỉ phương của đường thẳng tại đường link này bạn nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp