Cùng tìm hiểu Cách viết phương trình đường tròn đi qua 2 điểm – Toán 10 chuyên đề
Viết phương trình đường tròn (C) đi qua 2 điểm có bán kính R; hoặc đi qua 2 điểm tiếp xúc với đường thẳng (d); hoặc đi qua 2 điểm có tâm nằm trên đường thẳng (Δ) cũng là dạng toán phổ biến. Chúng ta sẽ cùng tìm hiểu cách giải bài tập dạng này ngay sau đây.
* Cách giải bài tập viết phương trình đường tròn (C) đi qua 2 điểm
Tùy từng trường hợp, bài sẽ cho đường tròn (C) đi qua 2 điểm có bán kính R;
hoặc đường tròn (C) có đường kính AB và tọa độ điểm A, điểm B;
hoặc đường tròn (C) đi qua 2 điểm và có tâm nằm trên đường thẳng (d);
hoặc đường tròn (C) đia qua 2 điểm và tiếp xúc với một đường thẳng (Δ);
Về cơ bản chúng ta cần thực hiện:
– Tìm toạ độ tâm I(a;b) của đường tròn (C)
– Tìm bán kính R của (C)
– Viết phương trình đường tròn (C) dạng: (x – a)2 + (y – b)2 = R2
Để dễ hiểu hơn, chúng ta cùng vận dụng vào giải một số bài tập minh họa.
* Ví dụ 1: Viết phương trình đường tròn (C) trong biết (C) đi qua 2 điểm AB với A(1;1), B(5,3) và nhận AB là đường kính.
* Lời giải:
– Vì đường tròn (C) có đường kính AB với A(1;1), B(5,3).
– Ta có toạ độ tâm I của (C) là trung điểm A,B là:
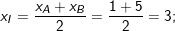
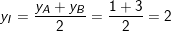
– Bán kính 
⇒ Đường tròn (C) có tâm I(3;2) và bán kính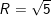 
có pt:
(x – 3)2 + (y – 2)2 = 5
* Ví dụ 2: Viết phương trình đường tròn (C) đi qua 2 điểm A(2;0), B(3;1) và có bán kính R = 5.
* Lời giải:
– Giả sử đường tròn (C) có tâm I(a;b)
Vì đường tròn (C) đi qua 2 điểm A, B nên ta có:
IA = 5 ⇒ IA2 = R2 = 25
⇒ (a – 2)2 + (b – 0)2 = 25
⇒ a2 – 4a + 4 + b2 = 25
⇒ a2 – 4a + b2 = 21 (1)
IB = 5 ⇒ IB2 = R2 = 25
⇒ (a – 3)2 + (b – 1)2 = 25
⇒ a2 – 6a + 9 + b2 – 2b + 1 = 15
⇒ a2 – 6a + b2 – 2b = 15 (2)
Lấy (1) trừ (2) vế với vế ta được:
2a + 2b = 6 ⇒ a + b = 3
⇒ a = 3 – b (3)
thay trở lại pt (1) ta có
(3 – b)2 – 4(3 – b) + b2 = 21
⇒ b2 – 6b + 9 – 12 + 4b + b2 = 21
⇒ 2b2 – 2b = 24
⇒ b2 – b -12 = 0
Giải phương trình bậc 2 với ẩn là b này ta được nghiệm b1 = -3 và b2 = 4
Với b = -3 thì từ pt (3) ⇒ a = 6 ⇒ I(6; -3)
Với b = 4 thì từ pt (3) ⇒ a = -1 ⇒ I(-1; 4)
Vậy ta có 2 đường tròn thỏa là:
(C1): (x – 6)2 + (y + 3)2 = 25
(C2): (x + 1)2 + (y – 4)2 = 25
* Ví dụ 3: Viết phương trình đường tròn (C) đi qua 2 điểm A(0;1), B(1;0) và có tâm nằm trên đường thẳng (d): x + y + 2 = 0
* Lời giải:
– Giả sử đường tròn (C) có tâm I(a;b),
Vì I(a,b) thuộc đường thẳng x + y + 2 = 0 nên ta có: a + b + 2 = 0 (1)
vì (C) đi qua 2 điểm A(0;1), B(1;0) nên ta có R = IA = IB ⇒ IA2 = IB2
⇒ (xA – xI)2 + (yA – yI)2 = (xB – xI)2 + (yB – yI)2
⇒ (a – 0)2 + (b – 1)2 = (a – 1)2 + (b – 0)2
⇒ a2 + b2 – 2b + 1 = a2 – 2a + 1 + b2
⇒ 2b = 2a ⇒ a = b (2)
thay vào pt (1) ta được a = b = -1
và R2 = IA2 = 12 + 22 = 5
Vậy phương trình đường tròn (C) đi qua 2 điểm A(0;1), B(1;0) và có tâm I(-1;-1) là:
(x + 1)2 + (y + 1)2 = 5
* Ví dụ 4: Viết phương trình đường tròn (C) đi qua 2 điểm A(-1;0), B(1,2) và tiếp xúc với đường thẳng (d): x – y – 1 = 0
* Lời giải:
– Gọi I(a;b) là tâm đường tròn và R là bán kính của đường tròn (C).
– Khi đó khoảng cách từ tâm I của (C) đến đường thẳng (d) là:
(1)
Vì A, B là 2 điểm thuộc đường tròn nên ta có:
(-1 – a)2 + b2 = R2 (2)
(1 – a)2 + (2 – b)2 = R2 (3)
Từ (2) và (3) có: (1 + a)2 + b2 = (1 – a)2 + (2 – b)2
⇒ 1 + 2a + a2 + b2 = 1 – 2a + a2 + 4 – 4b + b2
⇒ 2a + 1 = -2a – 4b + 5
⇒ 4a + 4b = 4
⇒ a + b = 1 (4)
Từ (1) và (2) lại có:
(a – b – 1)2 = 2[(1 + a)2 + b2]
⇒ 1 + a2 + b2 + 2ab – 6a – 2b = 0
⇒ 1 + (a + b)2 + 6(a + b) – 8b = 0
mà theo (4) thì: a + b = 1 nên
⇒ 1 + 12 + 6 – 8b = 0
⇒ b = 1 và từ (4) ⇒ a = 0
⇒ R2 = 2.
Vậy phương trình đường tròn (C) là: x2 + (y – 1)2 = 2
Như vậy với Cách viết phương trình đường tròn đi qua 2 điểm và ví dụ cụ thể ở trên, hy vọng bài viết giúp ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để ghi nhận và hỗ trợ, chúc các em học tập tốt.
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp
