Cách viết phương trình đường tròn đi qua 3 điểm – Toán 10 chuyên đề

Cùng tìm hiểu Cách viết phương trình đường tròn đi qua 3 điểm – Toán 10 chuyên đề

Để viết phương trình đường tròn đi qua 3 điểm, cách hay dùng nhất là ta lần lượt thay các giá trị các điểm này vào phương trình tổng quát của đường tròn, sau đó lập thành hệ 3 phương trình bậc nhất 3 ẩn. Giải hệ này thay các giá trị tìm được vào phương trình đường tròn, ta được kết quả. Cụ thể:

Giả sử phương trình đường tròn (C) có dạng: x² + y² – 2ax – 2by + c = 0. (*) (với điều kiện a² + b² – c > 0).

– Từ điều kiện bài toán: điểm A, B và C thuộc đường tròn nên thay tọa độ điểm A, B và C vào pt(*) ta được hệ ba phương trình bậc nhất với ẩn a; b; c.

– Giải hệ tìm a, b, c thay vào pt đường tròn (C).

* Ví dụ 1: Viết phương trình đường tròn (C) biết rằng (C) đi qua 3 điểm A(-1;3), B(3;5), C(4;-2)

* Lời giải:

Đường tròn (C) đi qua 3 điểm A(-1;3), B(3;5), C(4;-2)

– Goi (C) có dạng: x² + y² – 2ax – 2by + c = 0.

– Vì (C) đi qua A, B, C nên thay lần lượt toạ độ A, B, C vào pt đường tròn (C) ta có hệ sau:

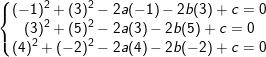
– Giải hệ trên ta được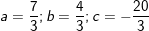 

⇒ Đường tròn (C) là: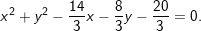 

* Ví dụ 2: Viết phương trình đường tròn (C) đi qua 3 điểm A(2; 1) ; B(2; 5) và C(-2; 1).

* Lời giải:

Đường tròn (C) đi qua 3 điểm  A(2; 1) ; B(2; 5) và C(-2; 1).

Gọi phương trình đường tròn (C) có dạng:

x² + y² – 2ax – 2by + c = 0 ( a² + b² – c > 0)

Vì các điểm A, B và C đều thuộc đường tròn (C).

A thuộc (C) nên: 4 + 1 – 4a – 2b + c = 0 (1)

B thuộc (C) nên: 4+ 25 – 4a – 10b + c = 0 (2)

C thuộc (C) nên: 4 + 1 + 4a – 2b + c = 0 (3)

Giải hệ (1), (2) và (3) ta được: a = 0; b = 3 và c = 1

Vậy phương trình đường tròn (C) có dạng:

x² + y² – 6y + 1 = 0

* Ví dụ 3: Viết phương trình đường tròn (C) đi qua 3 điểm A( 0; 4); B( 2; 4) và C( 4; 0)

* Lời giải:

Phương trình đường tròn (C) có dạng:

x² + y² – 2ax – 2by + c = 0 (với a² + b² – c > 0)

Vì 3 điểm A, B và C đều thuộc đường tròn (C) nên có:

Vậy PT đường tròn (C) có dạng:

x² + y² – 2x – 2y – 8 = 0

* Ví dụ 4: Viết phương trình đường tròn ngoại tiếp tam giác ABC biết A(-2; 4); B(5; 5) và C(6; -2)

* Lời giải:

– Gọi đường tròn ngoại tiếp tam giác là (C):

x² + y² + 2ax + 2by + c = 0 (với a² + b² – c > 0)

Do ba điểm A(-2; 4); B(5; 5) và C(6; -2) đều thuộc đường tròn, nên ta có:

Vậy đường tròn (C) cần tìm là: x² + y² – 4x – 2y – 20 = 0

* Lưu ý: 1. Ở ví dụ trên, việc gọi phương trình đường tròn thay vì x² + y² – 2ax – 2by + c = 0 ta cũng có thể gọi pt đường tròn có dạng: x² + y² + 2ax + 2by + c = 0 và kết quả bài toán cũng không thay đổi.

2. Sau khi viết được phương trình đường tròn đi qua 3 điểm, các em có thể xác định tâm của đường tròn, bán kính của đường tròn,… như vậy một số bài toán yêu cầu như:

– Tìm tọa độ tâm đường tròn đi qua 3 điểm;

– Tâm của đường tròn qua 3 điểm có thuộc đường thẳng (d) cho trước?

– Tìm bán kính đường tròn đi qua 3 điểm

thì trước tiên, các em cần viết phương trình đường tròn đi qua 3 điểm.

>> xem thêm: Các dạng toán về phương trình đường tròn

Như vậy với Cách viết phương trình đường tròn đi qua 3 điểm và ví dụ cụ thể ở trên, hy vọng bài viết giúp ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để .Vn ghi nhận và hỗ trợ, chúc các em học tập tốt.

Giáo Dục