Công thức hệ thức lượng trong tam giác vuông, cân, thường và bài tập
Bài viết hôm nay, sẽ giới thiệu đến các bạn công thức hệ thức lượng trong tam giác vuông, cân, thường và nhiều dạng bài tập thường gặp. Hãy dành thời gian tìm hiểu để nắm chắc hơn chuyên đề Hình học 12 vô cùng qua trọng này bạn nhé !
I. CÔNG THỨC HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
1. Các hệ thức về cạnh và đường cao trong tam giác vuông
Bạn đang xem: Công thức hệ thức lượng trong tam giác vuông, cân, thường và bài tập
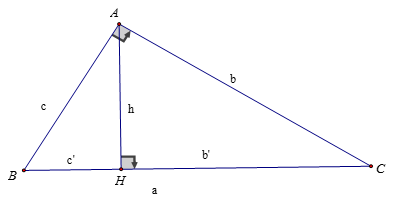
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
- BH = c’ được gọi là hình chiếu của AB xuống BC
- CH = b’ được gọi là hình chiếu của AC xuống BC
Khi đó, ta có:
- c2 = a.c’ (AB2 = BH.BC)
- b2 = a.b’ (AC2 = CH.BC)
- h2 = b’.c’ (AH2 = CH.BH)
- b.c = a.h (AB.AC = AH.BC )
- 1/h2 = 1/b2 + 1/c2 (1/AH2 = 1/AB2 + 1/AC2)
- b2 + c2 = a2 (AB2 + AC2 = BC2)(Định lý Pytago)
2. Tỉ số lượng giác của góc nhọn
a. Định nghĩa

- sinα = cạnh đối chia cho cạnh huyền
- cosα = cạnh kề chia cho cạnh huyền
- tanα = cạnh đối chia cho cạnh kề
- cotα = cạnh kề chia cho cạnh đối
b. Định lí
Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.
c. Một số hệ thức cơ bản

d. So sánh các tỉ số lượng giác
Cho góc nhọn α, ta có:
a) Cho α,β là hai góc nhọn. Nếu α < β thì
- sinα < sinβ; tanα < tanβ
- cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα
3. Hệ thức về góc và cạnh trong tam giác vuông
a. Các hệ thức
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
- Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
- Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề

- b = a.sinB = a.cosC
- c = a.sinC = a.cosB
- b = c.tanB = c.cotC
- c = b.tanB = b.cotC
4. Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác : Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.
Các bài toán về giải tam giác:
Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại
b) Giải tam giác khi biết hai cạnh và góc xen giữa
Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng định lí cosin để tính góc

Lưu ý:
- Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)
- Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.
II. CÔNG THỨC HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG
1. Định lý Cosin

Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
- a2 = b2 + c2 – 2bc.cosA;
- b2 = c2 + a2 – 2ca.cosB;
- c2 = a2 + b2 – 2ab.cosC.
Hệ quả:
- Cos A = (b2 + c2 – a2)/2bc
- Cos B = (a2 + c2 – b2)/2ac
- Cos C = (a2 + b2 – c2)/2ab
2. Định lý Sin
Trong tam giác ABC bất kể, tỉ số giữa một cạnh và sin của góc đối lập với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác. Ta có :
a /sinA = b/sinB = c/sinC = 2R
Với R là nửa đường kính đường tròn ngoại tiếp tam giác

Ngoài ra, những bạn nên tìm hiểu thêm thêm công thức lượng giác chi tiết cụ thể tại đây .
3. Độ dài đường trung tuyến của tam giác

Cho tam giác ABC có độ dài cạnh BC = a, CA = b, AB = c. Gọi ma, mb, mc lần lượt là độ dài những đường trung tuyến vẽ từ đỉnh A, B, C của tam giác. Ta có
- ma2 = [2(b2 + c2) – a2]/4
- mb2 = [2(a2 + c2) – b2]/4
- mc2 = [2(a2 + b2) – c2]/4
4. Công thức tính diện tích tam giác
Ta kí hiệu ha, hb và hc là những đường cao của tam giác ABClần lượt vẽ từ những đỉnh A, B, C và S là diện tích quy hoạnh tam giác đó .
Diện tích S của tam giác ABC được tính theo một trong những công thức sau :
- S = ½absinC = ½bcsinA = ½casinB
- S = abc/4R
- S = pr
- S = √p(p – a)(p – b)(p – c) (công thức hê – rông)
III. CÁC DẠNG BÀI TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG, CÂN, THƯỜNG
Ví dụ 1: Cho ΔABC có AB = 12, BC = 15, AC = 13
a. Tính số đo các góc của ΔABC
b. Tính độ dài các đường trung tuyến của ΔABC
c. Tính diện tích tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC
d. Tính độ dài đường cao nối từ các đỉnh của tam giác ABC

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác ta có:

c. Để tính được diện tích một cách chính xác nhất ta sẽ áp dụng công thức Hê – rông


IV. MỘT SỐ BÀI TẬP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC LUYỆN TẬP THÊM
Bài 1: Cho ∆ABC vuông tại A. Biết ABAC=57. Đường cao là AH = 15cm. Áp dụng hệ thức lượng trong tam giác vuông, hãy tính HB, HC.
Bài 2: Cho tam giác ABC vuông tại A. Trong đó AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC.
Bài 3: Cho ∆ABC vuông tại A. Kẻ đường cao AH, tính chu vi ∆ABC biết AH = 14cm, HBHC=14
Bài 4: Cho tam giác ABC vuông tại A. Có đường cao AH. Biết AB = 20cm, HC = 9cm. Tính độ dài AH.
Bài 5: Cho tam giác ABC vuông tại A có cạnh BD là phân giác góc B. Biết rằng AD = 2cm; BD = 12 cm. Tính độ dài cạnh BC.
Bài 6: Cho tam giác ABC , Góc B = 60 độ, BC = 8cm; AB + AC = 12cm. Tính độ dài cạnh AB.
Bài 7: Cho hình thang cân ABCD. Trong đó có đáy lớn của hình thang là CD = 10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên của hình thang. Tính độ dài đường cao của nó.
Bài 8:
a. Cho tam giác ABC có Góc B = 60 độ, Góc C = 50 độ, ?? = 35?? . Tính diện tích tam giác ABC.
b. Cho tứ giác ABCD có góc A = Góc D = 90 độ, Góc C = 40 độ, ?? = 4??, ?? = 3??. Tính diện tích tứ giác ABCD.
c. Cho tứ giác ABCD có các đường chéo cắt nhau tại vị trí O. Cho biết ?? = 4, ?? = 5, Góc AOB = 50 độ. Tính diện tích tứ giác ABCD bằng hàm thức lượng giác.
Bài 9: Cho ∆ABC vuông tại A, kẻ đường cao AH, chu vi tam giác AHB = 40cm, chu vi ∆ACH = 5dm. Tính cạnh BH, CH và chu vi ∆ABC.
Bài 10: Chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ lần lượt với 8, 15, 17.
a) Chứng minh đó là một tam giác vuông.
b) Tính khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác.
Bài viết trên đây, đã giới thiệu đến quý bạn đọc công thức hệ thức lượng trong tam giác vuông, cân, thường và nhiều dạng bài tập thường gặp. Hi vọng, chúng tôi đã cung cấp thêm cho bạn thêm nguồn tư liệu hữu ích giúp các bạn dạy và học tốt hơn. Xem thêm công thức tính tích phân đầy đủ & nhiều dạng bài tập thường gặp nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





