Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
Ở bài viết này, sẽ giới thiệu và chia sẻ chi tiết tới bạn đọc Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất cùng các dạng bài toán thường gặp. Mời các bạn cùng tham khảo để có thêm nguồn tư liệu quý nhé !
I. LÝ THUYẾT CHUNG
1. Mặt cầu là gì?
Bạn đang xem: Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
Mặt cầu: Có một điểm I cố định trong không gian, tập hợp những điểm A cách I một khoảng không đổi IA được gọi là mặt cầu tâm I, bán kính R = IA.
2. Khối cầu là gì?
Khối cầu: Tập hợp những điểm nằm trong mặt cầu và mặt cầu được gọi là hình cầu hay khối cầu có tâm I bán kính là R = IA.
II. CÔNG THỨC TÍNH THỂ TÍCH KHỐI CẦU (HÌNH CẦU)
Muốn tính thể tích khối cầu ta cần tìm kích thước bán kính của nó. Sau đó thay vào công thức V = ⁴⁄₃πr³ để tính. Nhớ ghi đơn vị của thể tích là đơn vị khối nhé (cm3, m3,…)
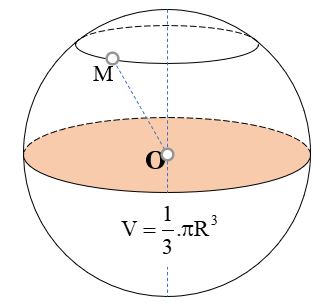
Trong đó:
-
V là thể tích khối cầu (đơn vị m3)
-
π là số pi, có giá trị sấp sỉ 3,14
-
r là bán kính khối cầu
dlà bánh kính mặt cầu/hình cầu
****CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU
Công thức tính diện tích mặt cầu là S = 4π.R2.
****TỔNG HỢP NHỮNG CÔNG THỨC CẦN GHI NHỚ

III. CÁCH TÍNH THỂ TÍCH KHỐI CẦU (HÌNH CẦU)
Để giải một bài toán tính thể tích khối cầu (hình cầu) các bạn thực hiện qua 3 bươc sau đây nhé !
Bước 1: Viết công thức tính thể tích hình cầu ra giấy nháp
V = ⁴⁄₃πr³
Bước 2: Tìm kích thước bán kính
Nếu trong đề bài toán có cho sẳn kích thước bán kính thì chúng ta đến bước tiếp theo.
Nếu đề bài cho đường kính thì bạn chia đôi để có được bán kính. Ví dụ, đường kính d = 10 cm, thì bán kính r = 5 cm.
Bước 3: Thay vào công thức tính thể tích hình cầu
Ví dụ: tìm được bán kính khối cầu r = 5 cm. Ta có,
Thể tích khối cầu V = ⁴⁄₃πr³ = 4/3.3,14.(5)³ = 523,3 cm³
IV: BÀI TẬP VỀ THỂ TÍCH KHỐI CẦU (HÌNH CẦU)
Câu 1:Cho hình tròn có chu vi là 31,4 cm. Hãy tính thể tích hình cầu có bán kính bằng bán kính của hình tròn vừa cho.
Giải:
Chu vi hình tròn C = 2πr = 31.4 cm
=> Bán kính r = C/2π = 5 cm
Thể tích khối cầu đã cho là:
V = ⁴⁄₃πr³ = 4/3.3,14.(5)³ = 523,3 cm³
Câu 2: Tính thể tích khối cầu có đường kính d = 4 cm.
Giải:
Bán kính r = d/2 = 2 cm
Thể tích khối cầu là:
V = ⁴⁄₃πr³ = 4/3.3,14.(2)³ = 33,49 cm³
Câu 3: Cho tứ diện đều ABCD có cạnh đáy bằng a. Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng:
Câu 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
Câu 5: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên bằng a. Bán kính của khối cầu ngoại tiếp hình chóp này bằng:
Câu 6: Thể tích khối cầu nội tiếp khối lập phương có cạnh bằng a là:
Câu 7: Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên cùng bằng a. Diện tích của hình cầu ngoại tiếp hình lăng trụ này bằng:
Câu 8: Thể tích của khối cầu ngoại tiếp khối lập phương có cạnh bằng a là:
Câu 9: Gọi (S) là mặt cầu có tâm O và bán kính r, d là khoảng cách từ O đến mặt phẳng (P), d < r. Khi đó có bao nhiêu điểm chung giữa (S), (P)?
| A. Vô số | B. 1 |
| C. 0 | D. 2 |
Câu 10: Cho mặt cầu có diện tích bằng . Khi đó, bán kính mặt cầu là:
Câu 11: Cho khối cầu có thể tích bằng . Khi đó bán kính khối cầu bằng:
Câu 12: Cho tứ diện DABC, đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Biết AB = 3a, BC = 4a, DA = 5a. bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng:
Câu 13: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a. diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng
Trên đây đã giới thiệu đến quý thầy cô và các bạn học sinh Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất cùng các dạng bài toán thường gặp. Hi vọng, chúng tôi đã cung cấp cho bạn thêm nhiều thông tin hữu ích. Công thức tính thể tích hình chóp cũng đã được chúng tôi chia sẻ rất chi tiết đó. Bạn tìm hiểu thêm nhé !
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp



