Định lí Viet tổng hợp đầy đủ nhất và cách ứng dụng trong giải toán

Định lí Viet tổng hợp đầy đủ nhất và cách ứng dụng trong giải toán

Bài viết hôm nay, sẽ tổng hợp định lí Viet(Vi-ét) cho phương trình bậc 2, bậc 3, bậc 4,…,bậc n cho bạn làm năm chắc hơn phần kiến thức Đại số vô cùng quan trọng này nhé ! Bên cạnh đó, chúng tôi còn hướng dẫn cách ứng dụng định lí Viet trong giải toán cực hay. Bạn tìm hiểu nhé !

A. ĐỊNH LÍ VIET, HỆ THỨC VIET LÀ GÌ?

Định lí Viet là công thức được tìm ra bởi nhà toán học người Pháp Francois Viète nê lên mỗi quan hệ giữa các nghiệm của một phương trình đa thức trong trường số phức và các hệ số của nó.

Bạn đang xem: Định lí Viet tổng hợp đầy đủ nhất và cách ứng dụng trong giải toán

Tê gọi của định lí phiên âm theo tiếng Việt là Vi-ét. Đây là phần kiến thức quan trọng trong chương trình Toán phổ thông.

B. ĐỊNH LÍ VIET (VI-ÉT) CHO PHƯƠNG TRÌNH BẬC 2, BẬC 3, BẬC 4…BẬC N

I. Định lý Viet thuận.

Cho phương trình bậc 2 một ẩn: ax²+bx+c=0 (a≠0) (*) có 2 nghiệm x₁ và x₂. Khi đó 2 nghiệm này thỏa mãn hệ thức sau:

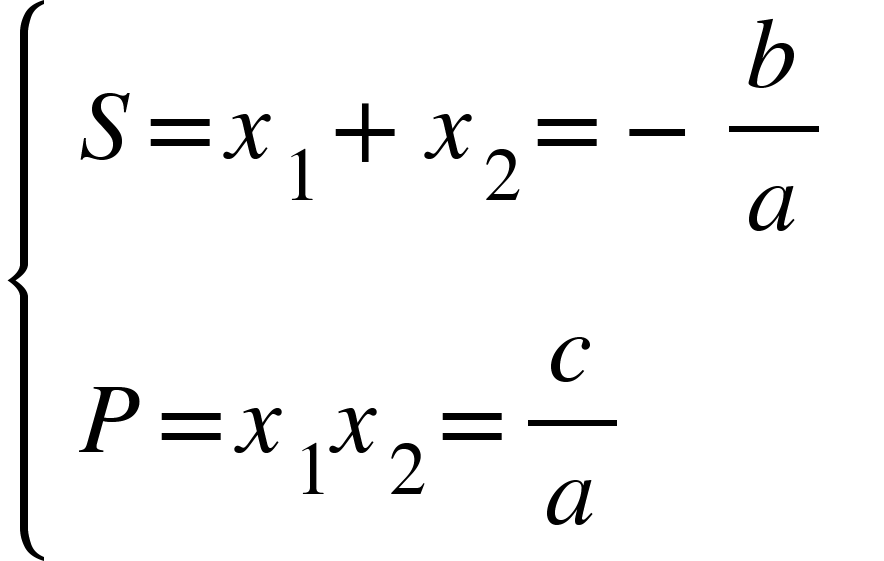
Hệ quả: Dựa vào hệ thức Viet khi phương trình bậc 2 một ẩn có nghiệm, ta có thể nhẩm trực tiếp nghiệm của phương trình trong một số trường hợp đặc biệt:

• Nếu a+b+c=0 thì (*) có 1 nghiệm x₁=1 và x₂=c/a
• Nếu a-b+c=0 thì (*) có nghiệm x₁=-1 và x₂=-c/a

II. Định lý Viet đảo.

Giả sử hai số thực x₁ và x₂ thỏa mãn hệ thức:

thì x₁ và x₂ là 2 nghiệm của phương trình bậc 2: x²-Sx+P=0 (1).

Chú ý: điều kiện S²-4P≥0 là bắt buộc. Đây là điều kiện để ∆(1)≥0  hay nói cách khác, đây là điều kiện để phương trình bậc 2 tồn tại nghiệm.

III. Tìm hiểu về định lý Viet bậc 2, bậc 3, bậc n

1. Hệ thức Viet bậc 2

Gọi nghiệm của phương trình bậc 2 lần lượt là x1 và x2, công thức Vi-ét thể hiện theo phương trình như sau:

PT: (ax^2 + bx + c = 0 (trong đó a # 0) thì ta có:  x1 + x2 = S = -b/a và x1.x2 = P = c/a

2. Hệ thức Viet bậc 3

Gọi nghiệm của phương trình bậc 3 lần lượt là x1, x2 và x3, công thức Vi-ét thể hiện theo phương trình như sau:

PT: ax^3 + bx^2 + cx + d  = 0 (x1, x2 và x3 là 3 nghiệm phân biệt), ta có:

• x1 + x2 + x3 = -b/a
• x1 x2 + x1 x3 + x1 x3 = c/a
• x1 x2 x3 = c/a

3. Hệ thức Viet bậc 4

Nếu phương trình bậc bốn: a(x2)2+bx3+cx2+dx+e=0 (a≠0) có 4 nghiệm x1, x2, x3 và x4, thì:

• x1 + x2 + x3 + x4 = -b/a
• x1 x2 + x1 x3 + x1 x4 + x2 x3 + x2 x4 + x3 x4 = c/a
• x1 x2 x3 + x1 x2 x4 + x1 x3 x4 + x2 x3 x4 = – d/a
• x1 x2 x3 x4 = e/a

Trong đó:

• x1, x2, x3 và x4 lần lượt là nghiệm của phương trình bậc 4
• a, b, c, d, e là các số đã biết sao cho a khác 0. a, b, c, d, e là những hệ số của phương trình đã cho và ta có thể phân biệt bằng cách gọi tương ứng với hệ số của x.
• a: hệ số bậc 4
• b: hệ số bậc 3
• c: hệ số bậc 2
• d: hệ số bậc 1
• e: hằng số (số hạng tự do)

C. ỨNG DỤNG CỦA ĐỊNH LÍ VIET TRONG GIẢI TOÁN

Bài viết trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn học sinh định lí Viet tổng hợp đầy đủ nhất và cách ứng dụng trong giải toán cực hay. Hi vọng chia sẻ cngf bài viết, bạn nắm chắc hơn chyên đề Đại số vô cùng qan trọng này. Xem thêm định lý Vi-et cho phương trình bậc 3 nữa bạn nhé !