Giải bài tập trang 42 Bài tập cuối chương 7 Biểu thức đại số sgk toán 7 tập 2 chân trời sáng tạo. Bài 4 Hãy viết một đa thức một biến bậc ba có 3 số hạng.
Bài 1 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Cho (A = {x^2}y + 2xy – 3{y^2} + 4). Tính giá trị của biểu thức A khi x = -2, y = 3.
Lời giải:
Bạn đang xem: Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 42 SGK Toán 7 tập 2 – CTST
(A = {x^2}y + 2xy – 3{y^2} + 4)
Thay các x = -2 và y = 3 vào công thức ta có :
(begin{array}{l}A = {( – 2)^2}.3 + 2( – 2).3 – {3.3^2} + 4\ = 4.3 – 12 – 27 + 4\ = – 23end{array})
Bài 2 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Trong các biểu thức sau, biểu thức nào là đơn thức một biến ?
a) 2y b) 3x + 5
c) 8 d)(21{t^{12}})
Lời giải:
Trong các biểu thức sau, biểu thức nào là đa thức một biến ?
(3 + 6y); (7{x^2} + 2x – 4{x^4} + 1);
(dfrac{2}{{x + 1}}); (dfrac{1}{3}x – 5).
Bài 3 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Trong các biểu thức sau, biểu thức nào là đa thức một biến ?
(3 + 6y); (7{x^2} + 2x – 4{x^4} + 1);
(dfrac{2}{{x + 1}}); (dfrac{1}{3}x – 5).
Lời giải:
Các đa thức 1 biến là :
(3 + 6y;7{x^2} + 2x – 4{x^4} + 1;dfrac{1}{3}x – 5)
Bài 4 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Hãy viết một đa thức một biến bậc ba có 3 số hạng.
Lời giải:
Có nhiều cách để viết một đa thức một biến bậc ba có 3 số hạng.
Chẳng hạn đa thức P(x) là đa thức một biến x bậc ba có 3 số hạng như sau:
P(x) = x3 + 3x2 + 1.
Bài 5 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Hãy cho biết bậc của các đa thức sau:
(A = 3x – 4{x^2} + 1)
(B = 7)
(M = x – 7{x^3} + 10{x^4} + 2)
Lời giải:
Đa thức A có hạng tử bậc cao nhất là -4x2 nên bậc của đa thức A bằng 2.
7 có bậc bằng 0 nên bậc của đa thức B bằng 0.
Đa thức M có hạng tử bậc cao nhất là 10x4 nên bậc của đa thức M bằng 4.
Bài 6 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Cho đa thức P(x) = ({x^3} + 27). Tìm nghiệm của P(x) trong tập hợp (left{ {0;3; – 3} right})
Lời giải:
Xét P(x) = ({x^3} + 27 = 0)
(begin{array}{l} Leftrightarrow {x^3} = – 27\ Leftrightarrow {x^3} = – 27 = {( – 3)^3}\ Rightarrow x = – 3end{array})
Vì ( – 3 in left{ {0;3; – 3} right}) nên -3 là 1 nghiệm
Bài 7 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Tam giác trong Hình 1 có chu vi bằng (25y – 8) cm. Tìm cạnh chưa biết trong tam giác đó.
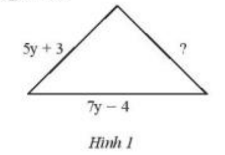
Lời giải:
Theo đề bài ta có chu vi hình tam giác = 25y – 8 cm
Ta có 2 cạnh của tam giác đã biết theo đề bài
( Rightarrow ) Cạnh còn lại cần tìm của tam giác là : 25y – 8 – 5y + 3 – 7y + 4 = 13y – 7 cm
Bài 8 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Cho đa thức (M(x) = 2{x^4} – 5{x^3} + 7{x^2} + 3x).
Tìm các đa thức N(x), Q(x) sao cho:
(N(x) – M(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7)
và (M(x) + Q(x) = 6{x^5} – {x^4} + 3{x^2} – 2)
Lời giải:
Theo đề bài ta có (M(x) = 2{x^4} – 5{x^3} + 7{x^2} + 3x)
(begin{array}{l}M(x) + Q(x) = 6{x^5} – {x^4} + 3{x^2} – 2\ Rightarrow Q(x) = (6{x^5} – {x^4} + 3{x^2} – 2) – (2{x^4} – 5{x^3} + 7{x^2} + 3x)\ Rightarrow Q(x) = 6{x^5} – {x^4} + 3{x^2} – 2 – 2{x^4} + 5{x^3} – 7{x^2} – 3x\Q(x) = 6{x^5} – 3{x^4} + 5{x^3} – 4{x^2} – 3x – 2end{array})
Theo đề bài ta có :
(begin{array}{l}N(x) – M(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7\ Rightarrow N(x) = – 4{x^4} – 2{x^3} + 6{x^2} + 7 + 2{x^4} – 5{x^3} + 7{x^2} + 3x\ Rightarrow N(x) = – 2{x^4} – 7{x^3} + 13{x^2} + 3x + 7end{array})
Bài 9 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Thực hiện phép nhân.
a) ((3x – 2)(4x + 5))
b) (({x^2} – 5x + 4)(6x + 1))
Lời giải:
a) ((3x – 2)(4x + 5))
(begin{array}{l} = 3x(4x + 5) – 2(4x + 5)\ = 3x.4x + 5.3x – 2.4x – 2.5\ = 12{x^2} + 7x – 10end{array})
b) (({x^2} – 5x + 4)(6x + 1))
(begin{array}{l} = {x^2}(6x + 1) – 5x(6x + 1) + 4(6x + 1)\ = {x^2}.6x + 1.{x^2} – 5x.6x – 5x.1 + 4.6x + 4.1end{array})
( = 6{x^3} – 29{x^2} + 19x + 4)
Bài 10 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Thực hiện phép chia.
a) ((45{x^5} – 5{x^4} + 10{x^2}):5{x^2})
b) ((9{t^2} – 3{t^4} + 27{t^5}):3t)
Lời giải:
a) ((45{x^5} – 5{x^4} + 10{x^2}):5{x^2})( = 9{x^3} – {x^2} + 2)

b) ((9{t^2} – 3{t^4} + 27{t^5}):3t = (27{t^5} – 3{t^4} + 9{t^2}):3t\=(27t^5):(3t) – (3t^4):(3t)+(9t^2):(3t) = 9{t^4} – 3{t^3}+3t)
Bài 11 trang 42 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2
Thực hiện phép chia.
a) ((2{y^4} – 13{y^3} + 15{y^2} + 11y – 3):({y^2} – 4y – 3))
b) ((5{x^3} – 3{x^2} + 10):({x^2} + 1))
Lời giải:

(a)(2{y^4} – 13{y^3} + 15{y^2} + 11y – 3):({y^2} – 4y – 3)=2y^2-5y+1)
b) ((5{x^3} – 3{x^2} + 10):({x^2} + 1)=5x-3+dfrac{-5x+13}{x^2+1})
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





