Giải bài 100, 101, 102 trang 92 SBT Toán 8 tập 1

Giải bài tập trang 92 bài 8 đối xứng tâm Sách bài tập (SBT) Toán 8 tập 1. Câu 100: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo…

Câu 100 trang 92 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O, vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.

Giải:                                                                           

Bạn đang xem: Giải bài 100, 101, 102 trang 92 SBT Toán 8 tập 1

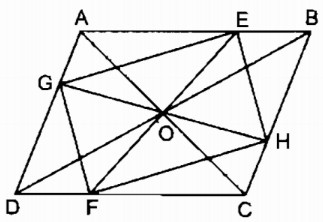
Xét ∆ OAE và ∆ OCF:

OA = OC (tính chất hình bình hành)

(widehat {AOE} = widehat {COF}) (đối đỉnh)

(widehat {OAE} = widehat {OCF}) (so le trong)

Do đó: ∆ OAE = ∆ OCF (g.c.g)

⇒ OE = OF (1)

Xét ∆ OAG và ∆ OCH:

OA = OC (tính chất hình bình hành)

(widehat {AOG} = widehat {COH}) (đối đỉnh)

(widehat {OAG} = widehat {OCH}) (so le trong)

Do đó: ∆ OAG = ∆ OCH (g.c.g)

⇒ OG = OH (2)

Từ (1) và (2) suy ra: Tứ giác EGFH là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Câu 101 trang 92 Sách bài tập (SBT) Toán 8 tập 1

Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a. Chứng minh rằng OB = OC

b. Tính số đo góc xOy để B đối xứng với C qua O.

Giải:                                                                      

a. Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.

⇒ OA = OB (tính chất đường trung trực) (1)

Vì C đối xứng với A qua trục Oy nên Oy là đường trung trực của đoạn AC.

⇒ OA = OC (tính chất đường trung trực) (2)

Từ (1) và (2) suy ra: OB = OC.

b. Ta có: OB = OC do đó điểm B đối xứng với điểm C qua tâm O cần thêm điều kiện B, O, C thẳng hàng.

∆ OAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của (widehat {AOB} Rightarrow {widehat O_1} = {widehat O_3})

∆ OAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của (widehat {AOC} Rightarrow {widehat O_2} = {widehat O_4})

B, O, C thẳng hàng ( Leftrightarrow {widehat O_1} = {widehat O_2} + {widehat O_3} + {widehat O_4} = {180^0})

(eqalign{&  Leftrightarrow 2{widehat O_1} + 2{widehat O_2} = {180^0}  cr&  Leftrightarrow {widehat O_1} + {widehat O_2} = {90^0}  cr&  Leftrightarrow widehat {xOy} = {90^0} cr} )

Vậy (widehat {xOy} = {90^0}) thì B đối xứng với C qua tâm O.

Câu 102 trang 92 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo góc ABK, ACK.

Giải:                                                                       

Ta có K là điểm đối xứng của H qua tâm M nên MK = MH

Xét tứ giác BHCK ta có:

BM = MC (gt)

MK = MH (chứng minh trên)

Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Suy ra: KB // CH, KC // BH

              CH ⊥ AB (gt)

Suy ra: KB ⊥ AB nên (widehat {KBA} = {90^0})

BH ⊥ AC (gt)

Suy ra : CK ⊥ AC nên (widehat {KCA} = {90^0})

Trường

Giải bài tập