Giải bài 11, 12, 13, 14 trang 81 SBT Toán 8 tập 1

Giải bài tập trang 81 bài 2 hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 1: Tính các góc của hình thang ABCD (AB//CD), biết rằng…

Câu 11 trang 81 Sách bài tập (SBT) Toán 8 tập 1

Tính các góc của hình thang ABCD (AB//CD), biết rằng (widehat A = 3widehat D,widehat B – widehat C = {30^0})

Giải:

Bạn đang xem: Giải bài 11, 12, 13, 14 trang 81 SBT Toán 8 tập 1

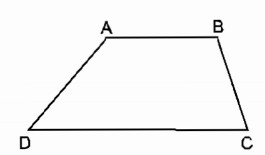
AB//CD

( Rightarrow widehat A + widehat D = {180^0})  (hai góc trong cùng phía)

Ta có: (widehat A = 3widehat D)  (gt)

(eqalign{
& Rightarrow 3widehat D + widehat D = {180^0} cr 
& Rightarrow widehat D = {45^0} cr 
& Rightarrow widehat A = {3.45^0} = {135^0} cr} )

(widehat B + widehat C = {180^0}) (hai góc trong cùng phía)

(widehat B – widehat C = {30^0}) (gt)

(eqalign{
& Rightarrow 2widehat B = {210^0} Rightarrow widehat B = {105^0} cr 
& widehat C = widehat B – {30^0} = {105^0} – {30^0} = {75^0} cr} )

Câu 12 trang 81 Sách bài tập (SBT) Toán 8 tập 1

Tứ giác ABCD có BC=CD và DB là tia phân giác của góc D. Chứng minh rằng ABCD là hình thang

Giải:

∆ BCD có BC = CD (gt) nên ∆ BCD cân tại C

( Rightarrow {widehat B_1} = {widehat D_1}) (tính chất tam giác cân)

Mà ({widehat D_1} = {widehat D_2})

Suy ra: ({widehat B_1} = {widehat D_2})

Do đó: BC//AD (vì có cặp góc ở vị trí so le trong bằng nhau)

Vậy ABCD là hình thang (theo định nghĩa)

Câu 13 trang 81 Sách bài tập (SBT) Toán 8 tập 1

Dùng thước và êke kiểm tra xem trong các tứ giác trên hình 2:

a. Tứ giác nào chỉ có một cặp cạnh song song;

b. Tứ giác nào có hai cặp cạnh song song;

c. Tứ giác nào là hình thang.

Giải:

a. Tứ giác ở hình (1) chỉ có 1 cặp cạnh đối song song.

b. Tứ giác ở hình (3) có hai cặp cạnh đối song song.

c. Tứ giác ở hình (1) và hình (3) là hình thang.

Câu 14 trang 81 Sách bài tập (SBT) Toán 8 tập 1

Tính các góc B và D của hình thang ABCD, biết rằng (widehat A = {60^0},widehat C = {130^0}.)

Giải:

Hình thang ABCD ta có, (widehat A) và (widehat C) là hai góc đối

a. Trường hợp (widehat A) và (widehat B)  là hai góc kề với cạnh bên.

⇒ AB // BC

(widehat A + widehat B = {180^0}) (hai góc trong cùng phía bù nhau) 

( Rightarrow widehat B = {180^0} – widehat A = {180^0} – {60^0} = {120^0})

(widehat C + widehat D = {180^0}) (hai góc trong cùng phía bù nhau)

( Rightarrow widehat D = {180^0} – widehat C = {180^0} – {130^0} = {50^0}) 

b. Trường hợp (widehat A) và (widehat D) là 2 góc kề với hai cạnh bên

⇒ AB // CD

(widehat A + widehat D = {180^0}) (hai góc trong cùng phía bù nhau)  

( Rightarrow widehat D = {180^0} – widehat A = {180^0} – {60^0} = {120^0})

(widehat B + widehat C = {180^0}) (hai góc trong cùng phía bù nhau)

( Rightarrow widehat B = {180^0} – widehat C = {180^0} – {130^0} = {50^0})

Trường

Giải bài tập