Giải bài 140, 141, 142, 143 trang 97 SBT Toán 8 tập 1

Giải bài tập trang 97 bài 11 hình thoi Sách bài tập (SBT) Toán 8 tập 1. Câu 140: Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì ? Vì sao ?…

Câu 140 trang 97 Sách bài tập (SBT) Toán 8 tập 1

Hình thoi ABCD có (widehat A = {60^0}) . Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì ? Vì sao ?

Giải:                                                            

Bạn đang xem: Giải bài 140, 141, 142, 143 trang 97 SBT Toán 8 tập 1

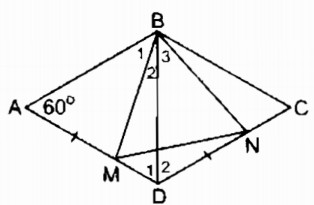
Nối BD, ta có:

AB = AD (gt)

nên ∆ ABD cân tại A

mà  (widehat A = {60^0})

⇒ ∆ ABD đều

( Rightarrow widehat {ABD} = {widehat D_1} = {60^0})  và BD = AB

Suy ra: BD = BC = CD

⇒ ∆ CBD đều

( Rightarrow {widehat D_2} = {60^0})

Xét ∆ BAM và ∆ BDN:

AB = BD (chứng minh trên)

(widehat A = {widehat D_2} = {60^0})

AM = DN

Do đó: ∆ BAM = ∆ BDN (c.g.c) ( Rightarrow {widehat B_1} = {widehat B_3})  và BM = BN

Suy ra: ∆ BMN cân tại B

({widehat B_2} + {widehat B_1} = widehat {ABD} = {60^0})

Suy ra: ({widehat B_2} + {widehat B_3} = widehat {MBN} = {60^0})

Vậy ∆ BMN đều

 

---

Câu 141 trang 97 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC. Lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K theo thứ tự là trung điểm của BE, CD, DE, BC. Chứng minh rằng IK vuông góc với MN.

Giải:                                                              

Trong ∆ BCD ta có:

K là trung điểm của BC (gt)

N là trung điểm của CD (gt)

nên NK là đường trung bình của ∆ BCD

⇒ NK // BD và NK =({1 over 2})BD (1)

Trong ∆ BED ta có:

M là trung điểm của BE (gt)

I là trung điểm của DE (gt)

nên MI là đường trung bình của ∆ BED

⇒ MI // BD và MI =({1 over 2})BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MI // NK và MI = NK

nên tứ giác MKNI là hình bình hành

Trong ∆ BEC ta có:

MK là đường trung bình

 MK = ({1 over 2})CE (tính chất đường trung bình của tam giác)    

BD = CE (gt)

Suy ra: MK = KN

Vây hình bình hành MKNI là hình thoi.

⇒ IK ⊥ MN (tính chất hình thoi)

 

---

Câu 142 trang 97 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD, các đường chéo cắt nhau ở O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, COD, DOA. Chứng minh rằng EFGH là hình thoi.

Giải:                                                                         

Ta có: (widehat {AOB} = widehat {COD}) (đối đỉnh)

(widehat {EOB} = {1 over 2}widehat {AOB}) (gt)

(widehat {COG} = {1 over 2}widehat {COD}) (gt)

Suy ra: (widehat {EOB} = widehat {COG})

(widehat {EOB} + widehat {BOC} + widehat {COG} = 2widehat {EOB} + widehat {BOC})

mà (widehat {AOB} + widehat {BOC} = {180^0}) (kề bù)

hay (2widehat {EOB} + widehat {BOC} = {180^0})

Suy ra: E, O, G thẳng hàng

Ta lại có: (widehat {BOC} = widehat {AOD}) (đối đỉnh)

(widehat {HOD} = {1 over 2}widehat {AOD}) (gt)

(widehat {FOC} = {1 over 2}widehat {BOC}) (gt)

Suy ra: (widehat {HOD} = widehat {FOC})

(widehat {HOD} + widehat {COD} + widehat {FOC} = 2widehat {HOD} + widehat {COD})

mà (widehat {AOD} + widehat {COD} = {180^0}) (kề bù)

hay(2widehat {HOD} + widehat {COD} = {180^0})             

Suy ra: H, O, F thẳng hàng

(widehat {ADO} = widehat {CBO}) (so le trong)

(widehat {HDO} = {1 over 2}widehat {ADO}) (gt)

(widehat {FBO} = {1 over 2}widehat {CBO}) (gt)

Suy ra: (widehat {HDO} = widehat {FBO})

– Xét ∆ BFO và ∆ DHO:

(widehat {HDO} = widehat {FBO}) (chứng minh trên_

OD = OB (tính chất hình bình hành)

(widehat {HOD} = widehat {FOB}) (đối đỉnh)

Do đó: ∆ BFO = ∆ DHO (g.c.g)

⇒ OF = OH

(widehat {OAB} = widehat {OCD}) (so le trong)

(widehat {OAE} = {1 over 2}widehat {OAB}) (gt)

(widehat {OCG} = {1 over 2}widehat {OCD}) (gt)

Suy ra: (widehat {OAE} = widehat {OCG})       

– Xét ∆ OAE và ∆ OCG:

(widehat {OAE} = widehat {OCG}) (chứng minh trên)

OA = OC (tính chất hình bình hành)

(widehat {EOA} = widehat {GOC}) (đối đỉnh)

Do đó: ∆ OAE = ∆ OCG (g.c.g)

⇒ OE = OG

Suy ra: Tứ giác EFGH là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

OE ⊥ OF (tính chất hai góc kề bù)

hay EG ⊥ FH

Vậy: Tứ giác EFGH là hình thoi.

 

---

Câu 143 trang 97 Sách bài tập (SBT) Toán 8 tập 1

Dựng hình thoi ABCD, biết cạnh bằng 2cm, một đường chéo bằng 3cm.

Giải:                                                                       

Cách dựng:

       – Dựng ∆ ABD biết AB = AD = 2(cm), BD = 3cm

       – Trên nửa mặt phẳng bờ BD không chứa điểm A. Từ B dựng tia Bx // AD, từ D dựng tia Dy // AB, chúng cắt nhau tại C.

Ta có hình thoi ABCD cần dựng

Chứng minh:

Vì AB // CD và AD // BC nên tứ giác ABCD là hình bình hành

AB = AD = 2cm. Vậy tứ giác ABCD là hình thoi

Lại có: BD = 3cm

Hình thoi dựng được thỏa mãn điều kiện bài toán.

Trường

Giải bài tập