Giải bài 15, 16, 17, 18 trang 67 SGK toán 8 tập 2

Giải bài tập trang 67 bài 3 Tính chất đường phân giác của tam giác Sách giáo khoa toán 8 tập 2. Câu 15: Tính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất…

Bài 15 trang 67 – Sách giáo khoa toán 8 tập 2

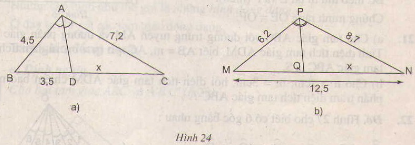
Tính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.

Bạn đang xem: Giải bài 15, 16, 17, 18 trang 67 SGK toán 8 tập 2

Giải:

a) AD là tia phân giác của ∆ABC nên 

(frac{BD}{AB}) = (frac{DC}{AC}) => DC = (frac{BD.AC}{AB}) = (frac{3,5.7,2}{4,5})

=> x = 5,6

b) PQ là đường phân giác của ∆PMN nên (frac{MQ}{MP}) = (frac{NQ}{NP}) 

Hay  (frac{MP}{6,2}) = (frac{x}{8,7})

Áp dụng tính chất của tỉ lệ thức:

=> (frac{x}{8,7}) = (frac{MP}{6,2}) = (frac{x + MQ}{8,7+ 6,2}) = (frac{12,5}{14,9})

=> x≈ 7,3

Bài 16 trang 67 – Sách giáo khoa toán 8 tập 2

Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng (frac{m}{n}).

Giải:

Kẻ AH ⊥ BC 

Ta có: 

S_ABD = (frac{1}{2})AH.BD

S_ADC  = (frac{1}{2})AH.DC

=>(frac{S_{SBD}}{S_{ADC}}) = (frac{frac{1}{2}AH.BD}{frac{1}{2}AH.DC}) = (frac{BD}{DC})

Mặt khác: AD là đường phân giác của ∆ABC

=> (frac{BD}{DC})= (frac{AB}{AC}) = (frac{m}{n}).

Vậy (frac{S_{SBD}}{S_{ADC}}) = (frac{m}{n})

Bài 17 trang 68 – Sách giáo khoa toán 8 tập 2

Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC(h25)

Giải:

Ta có MD là đường phân giác của tam giác ABM

=> (frac{AD}{BD}) = (frac{AM}{BM}) (1)

ME là đường phân giác của tam giác ACM

=> (frac{AE}{CE}) = (frac{AM}{MC}) (2)

Mà MB = MC( AM là đường trung tuyến)

=> (frac{AM}{BM}) = (frac{AM}{MC}) (3)

từ 1,2,3 => (frac{AD}{BD}) = (frac{AE}{CE}) => DE // BC( Định lí Talet đảo)

Bài 18 trang 68 – Sách giáo khoa toán 8 tập 2

Tam giác ABC có AB= 5cm, AC= 6cm, BC= 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.

Giải:

AE là đường phân giác của tam giác ABC nên 

(frac{AE}{AB}) = (frac{EC}{AC}) 

Áp dụng tính chất tỉ lệ thức

(frac{AE}{AB}) = (frac{EC}{AC}) = (frac{EB+EC}{AB+AC})= (frac{BC}{AB+AC})  

=> EB = (frac{AB.BC}{AB+AC}) = (frac{5.7}{5+6})

EC = BC- BE ≈ 3,8

Trường

Giải bài tập