Giải bài 19, 20, 21, 22, 23 trang 47 SGK toán 8 tập 2

Giải bài tập trang 47 bài 4 Bất phương trình bậc nhất một ẩn sgk toán 8 tập 2. Câu 19: Giải các bất phương trình theo quy tắc chuyển vế:…

Bài 19 trang 47 sgk toán 8 tập 2

Giải các bất phương trình theo quy tắc chuyển vế:

a) x – 5 > 3;                   b) x – 2x

Bạn đang xem: Giải bài 19, 20, 21, 22, 23 trang 47 SGK toán 8 tập 2

c) -3x > -4x + 2;             d) 8x + 2

Hướng dẫn giải:

a) x – 5 > 3 x > 5 + 3 x > 8

Vậy nghiệm của bất phương trình là x > 8

b) x – 2x x – 2x + 2x x

 Vậy nghiệm của bất phương trình là x

c) -3x > -4x + 2 -3x + 4x > 2 x > 2

 Vậy nghiệm của bất phương trình là x > 2

d) 8x + 2 8x – 7x x

Vậy nghiệm của bất phương trình là x

Bài 20 trang 47 sgk toán 8 tập 2

 Giải các bất phương trình (theo quy tắc nhân):

a) 0,3x > 0,6;              b) -4x

c) -x > 4;                     d) 1,5x > -9.

Hướng dẫn giải:

a) 0,3x > 0,6 ( frac{10}{3}).0,3x > 0,6.( frac{10}{3})

                    x > 2

Vậy  nghiệm của bất phương trình là x> 2

b) -4x  ( -frac{1}{4}).(-4x) > 12.(( -frac{1}{4})) x > -3

Vậy nghiệm của bất phương trình là x > -3

c) -x > 4 x

Vậy nghiệm của bất phương trình là x

d) 1,5x > -9  ( frac{3}{2})x > -9 ( frac{2}{3}).( frac{3}{2})x > (-9).( frac{2}{3})  x > -6

Vậy nghiệm của bất phương trình là x > -6

Bài 21 trang 47 sgk toán 8 tập 2

Giải thích sự tương đương sau:

a) x – 3 > 1 x + 3 > 7;            b) -x 3x > -6

Hướng dẫn giải:

a) x – 3 > 1 x + 3 > 7

Hai bất phương trình tương đương vì cộng 6 vào cả hai vế.

b) -x 3x > -6

Hai bất phương trình tương đương vì nhân -3 vào cả hai vế và đổi dấu bất phương trình.

Bài 22 trang 47 sách giáo khoa toán 8 tập 2

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) 1,2x 2x + 3

Hướng dẫn giải:

a) 1,2x x x

Vậy tập nghiệm của bất phương trình là S = {x/x

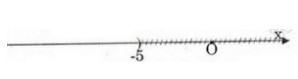
b) 3x + 4 > 2x + 3 3x – 2x > 3 -4 x > -1

Vậy tập hợ nghiệm của bất phương trình là S = {x/x > -1} và được biểu diễn trên trục số như sau:

Bài 23 trang 47 sgk toán 8 tập 2

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) 2x – 3 > 0;                  b) 3x + 4

c) 4 – 3x ≤ 0;                  d) 5 – 2x ≥ 0.

Hướng dẫn giải:

 a) 2x – 3 > 0 2x > 3 x >

Vậy tập nghiệm của bất phương trình là S = {x/x > } và được biểu diễn trên trục số như sau: 

b) 3x + 4 x

Vậy tập nghiệm của bất phương trình là S = {x/x } và được biểu diến trên trục số như sau:

c) 4 – 3x ≤ 0 x ≥  

 Vậy tập nghiệm của bất phương trình là S = {x/x ≥ } và được biểu diễn trên trục số như sau:

d)  5 – 2x ≥ 0 5 ≥ 2x x ≤  

Vậy tập nghiệm của bất phương trình là S = {x/x ≤ } và được biểu diến trên trục số như sau:

Trường

Giải bài tập