Giải bài tập trang 82, 83 bài 3 hình thang cân Sách bài tập (SBT) Toán 8 tập 1. Câu 22: Hình thang cân ABCD có AB// CD, AB
Câu 22 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có AB// CD, AB
Giải:
Bạn đang xem: Giải bài 22, 23, 24, 25 trang 82, 83 SBT Toán 8 tập 1
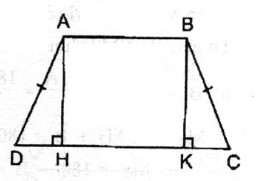
Xét hai tam giác vuông AHD và BKC:
(widehat {AHD} = widehat {BKC} = {90^0})
AD=BC (tính chất hình thang cân)
(widehat C = widehat D) (gt)
Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
Câu 23 trang 82 Sách bài tập (SBT) Toán 8 tập 1
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA=OB, OC=OD.
Giải:

Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
(widehat {ADC} = widehat {BCD}) (gt)
DC cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.g.c)
( Rightarrow {widehat C_1} = {widehat D_1})
Trong ∆ OCD ta có: ({widehat C_1} = {widehat D_1})
⇒ ∆ OCD cân tại O
⇒ OC = OD (1)
AC = BD ( tính chất hình thang cân)
⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO
Câu 24 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a. Tứ giác BMNC là hình gì ? Vì sao ?
b. Tính các góc của tứ giác BMNC biết rằng (widehat A = {40^0})
Giải:

a. ∆ ABC cân tại A
( Rightarrow widehat B = widehat C = {{{{180}^0} – widehat A} over 2}) (tính chất tam giác cân) (1)
AB = AC (gt)
⇒ AM + BM= AN+ CN
⇒ mà BM = CN (gt)
⇒ suy ra: AM = AN
⇒ ∆ AMN cân tại A
( Rightarrow {widehat M_1} = {widehat N_1} = {{{{180}^0} – widehat A} over 2}) ( tính chất tam giác cân) (2)
⇒ Từ (1) và (2) suy ra: ({widehat M_1} = widehat B)
⇒MN // BC ( vì có các cặp góc đồng vị bằng nhau)
Tứ giác BCMN là hình thang có (widehat B = widehat C). Vậy BCMN là hình thang cân.
b. (widehat B = widehat C = {{{{180}^0} – widehat A} over 2} = {{{{180}^0} – {{40}^0}} over 2} = {70^0})
Mà ({widehat M_2} + widehat B = {180^0}) (hai góc trong cùng phía)
( Rightarrow {widehat M_2} = {180^0} – widehat B = {180^0} – {70^0} = {110^0})
({widehat N_2} = {widehat M_2} = {110^0}) (tính chất hình thang cân)
Câu 25 trang 83 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
Giải:

Xét hai tam giác AEB và AFC
Có AB = AC (∆ ABC cân tại A)
(widehat {ABE} = {{widehat B} over 2} = {{widehat C} over 2} = widehat {ACF}) và (widehat A) là góc chung
( Rightarrow Delta ADB = Delta AECleft( {g.c.g} right) Rightarrow AE = AF Rightarrow Delta AEF) cân tại A
( Rightarrow widehat {AFE} = {{{{180}^0} – widehat A} over 2}) và trong tam giác (Delta ABC:,,widehat B = {{{{180}^0} – widehat A} over 2})
( Rightarrow widehat {AFE} = widehat B Rightarrow FE//BC) ⟹ tứ giác BFEC là hình thang.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





