Giải bài 24, 25, 26, 27 trang 160 SBT Toán 9 tập 2

Giải bài tập trang 160 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 24: Cho hình 74, trong đó MN = PQ. Chứng minh rằng…

Câu 24 trang 160 Sách bài tập (SBT) Toán 9 Tập 1 

Cho hình 74, trong đó MN = PQ. Chứng minh rằng:

a)      AE = AF;                                b) AN = AQ.

Bạn đang xem: Giải bài 24, 25, 26, 27 trang 160 SBT Toán 9 tập 2

Giải:

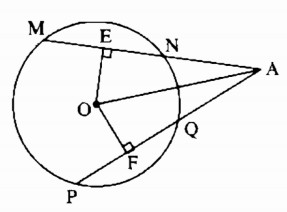
a) Nối OA

Ta có: MN = PQ (gt)

Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OAE và OAF, ta có:

(widehat {OEA} = widehat {{rm{OF}}A} = 90^circ )

      OA chung

      OE = OF ( chứng minh trên)

Suy ra: ∆OAE = ∆OAF (cạnh huyền, cạnh góc vuông)

Suy ra: AE = AF

b) Ta có: OE ⊥ MN (gt)

Suy ra: (EN = {1 over 2}MN) (đường kính vuông góc với dây cung)  (1)

            OF ⊥PQ (gt)

Suy ra: (FQ = {1 over 2}PQ) (đường kính vuông góc với dây cung)    (2)

Mặt khác: MN = PQ (gt)                                          (3)

Từ (1), (2) và (3) suy ra: EN = FQ                           (4)

Mà AE = QF ( chứng minh trên)                              (5)

Từ (4) và (5) suy ra:  AN + NE = AQ + QF              (6)

Từ (5) và (6) suy ra: AN = AQ.

Câu 25 trang 160 Sách bài tập (SBT) Toán 9 Tập 1

Cho hình 75, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây.

Giải:

Kẻ OH ⊥ CD, OK ⊥EF

Vì tứ giác OKIH có ba góc vuông nên nó là hình chữ nhật.

Ta có: CD = EF (gt)

Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)

Suy ra tứ giác OKIH là hình vuông.

Ta có:

CD = CI + ID = 2 + 14 =16 (cm)

(HC = HD = {{CD} over 2} = 8) (cm) (đường kính dây cung)

        IH = HC – CI = 8 – 2 = 6 (cm)

Suy ra: OH = OK = 6 (cm)  (OKIH là hình vuông).

Câu 26 trang 160 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O), dây AB và dây CD, AB

Chứng minh rằng KM

Giải:

Kẻ OI ⊥ AB, OE ⊥ CD

Trong ( O ; OA) ta có: AB

Suy ra: OI > OE (dây lớn hơn gần tâm hơn)

Trong (O ; OK) ta có: OI > OE (cmt)

Suy ra: KM

Câu 27 trang 160 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.

Giải:

Gọi CD là dây bất kì đi qua I và CD không vuông góc với OI.

Kẻ OK ⊥ CD

Tam giác OKI vuông tại K nên OI > OK

Suy ra: AB

Vậy dây AB vuông góc với IO tại I ngắn hơn mọi dây khác đi qua I.

Trường

Giải bài tập