Giải bài 25, 26, 27, 28 trang 80 SGK toán 8 tập 1

Giải bài tập trang 80 bài 4 Đường trung bình của tam giác, của hình thang sgk toán 8 tập 1. Câu 25: Hình thang ABCD có đáy AB, CD…

Bài 25 trang 80 sgk toán 8 tập 1

Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

Bài giải:

Bạn đang xem: Giải bài 25, 26, 27, 28 trang 80 SGK toán 8 tập 1

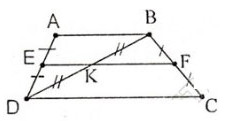
Ta có EA = ED, KB = KD (gt)

Nên EK // AB

Lại có FB = FC, KB = KD (gt)

Nên KF // DC // AB

Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.

Bài 26 trang 80 sgk toán 8 tập 1

Tính x, y trên hình 45, trong đó AB // CD // EF // GH.

Bài giải:

AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.

Do đó: CD = (frac{AB+EF}{2}) = (frac{8+16}{2}) = 12

Hay x = 12

Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.

Nên EF = (frac{CD+GH}{2})  => GH = 2EF -CD = 2.16 – 12

GH = 20 hay y = 20

Vậy x = 12, y = 20

Bài 27 trang 80 sgk toán 8 tập 1

Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB.

b) Chứng minh rằng EF  ≤ (frac{AB+CD}{2})

Bài giải:

a) Trong ∆ACD có EA = ED, KA = KC (gt)

nên EK là đường trung bình của ∆ACD

Do đó EK = (frac{CD}{2})

Tương tự KF là đường trung bình của ∆ABC.

Nên KF = (frac{AB}{2})

b) Ta có EF  ≤ EK + KF (bất đẳng thức trong ∆EFK)

Nên EF ≤ EK + KF = (frac{CD}{2}) + (frac{AB}{2}) = (frac{AB+CD}{2})

Vậy EF ≤ (frac{AB+CD}{2}).

Bài 28 trang 80 sgk toán 8 tập 1

Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thằng EF cắt BD ở I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Bài giải:

a) Vì EA = ED, FB = FC (gt)

Nên EF là đường trung bình của hình thang ABCD.

Do đó: EF // AB // CD

 ∆ABC có BF = FC và FK // AB

                          nên: AK = KC

               ∆ABD có AE = ED và EI // AB

nên: BI = ID

b) Vi EF là đường trung bình của hình thang ABCD.

nên EF = (frac{AB+CD}{2}) = (frac{6+10}{2}) = 8

EI là đường trung bình của ∆ABD nên EI = (frac{1}{2}).AB = (frac{1}{2}).6 = 3 (cm)

KF là đường trung bình của  ∆ABC  nên KF = (frac{1}{2}).AB = (frac{1}{2}).6 = 3 (cm)

Lại có EF = EI + IK + KF

nên IK = EF – (EI + KF) = 8 – (3 + 3) = 2 (cm)

Giải bài tập