Giải bài 26, 27, 28 trang 83 SBT Toán 8 tập 1

Giải bài tập trang 83 bài 3 hình thang cân Sách bài tập (SBT) Toán 8 tập 1. Câu 26: Chứng minh rằng hình thang có hai đường chéo bằng nhau là hình thang cân….

Câu 26 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng hình thang có hai đường chéo bằng nhau là hình thang cân.

Giải:

Bạn đang xem: Giải bài 26, 27, 28 trang 83 SBT Toán 8 tập 1

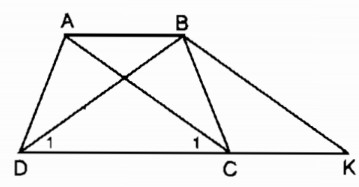
Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.

Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK

Mà AC = BD (gt)

Suy ra: BD = BK do đó ∆ BDK cân tại B

( Rightarrow {widehat D_1} = widehat K) (tính chất tam giác cân)

Ta lại có: ({widehat C_1} = widehat K) (hai góc đồng vị)

Suy ra:  ({widehat D_1} = {widehat C_1})

Xét ∆ ACD và ∆ BDC:

AC = BD (gt)

({widehat D_1} = {widehat C_1}) (chứng minh trên)

CD cạnh chung

Do đó: ∆ ACD = ∆ BDC (c.g.c) ( Rightarrow widehat {ADC} = widehat {BCD})   

Hình thang ABCD có (widehat {ADC} = widehat {BCD}) nên là hình thang cân.

Câu 27 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Tính các góc của hình thang cân, biết một góc bằng  ({50^0})

Giải:  

Giả sử hình thang cân ABCD có AB // CD và  (widehat D = {50^0})

Vì (widehat C = widehat D) (tính chất hình thang cân)

( Rightarrow widehat C = {50^0})

(widehat A + widehat D = {180^0}) (hai góc trong cùng phía)

( Rightarrow widehat A = {180^0} – widehat D = {180^0} – {50^0} = {130^0})

(widehat B = widehat A) (tính chất hình thang cân) (Rightarrow widehat B = {130^0})     

Câu 28 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.

Giải:

AB = AD (gt)

AD = BC (tính chất hình thang cân)

⇒ AB = BC do đó ∆ ABC cân tại B

(Rightarrow {widehat A_1} = {widehat C_1}) (tính chất tam giác cân)

Mặt khác: AB // CD (gt)

({widehat A_1} = {widehat C_2}) (hai góc so le trong)

Suy ra: ({widehat C_1} = {widehat C_2})

Vậy CA là tia phân giác của (widehat {BCD}).

Câu 29 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao ?

Giải:

Ta có: OA = OC (gt)

⇒ ∆ OAC cân tại O

( Rightarrow {widehat A_1} = {{{{180}^0} – widehat {AOC}} over 2}) (tính chất tam giác cân)   (1)

OB = OD (gt)

⇒ ∆ OBD cân tại O

( Rightarrow {widehat B_1} = {{{{180}^0} – widehat {BOD}} over 2}) (tính chất tam giác cân)   (2)

(widehat {AOC} = widehat {BOD}) (đối đỉnh)  (3)

Từ (1), (2) và (3) suy ra: ({widehat A_1} = {widehat B_1})

⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)

Suy ra: Tứ giác ACBD là hình thang

Ta có: AB = OA + OB

            CD = OC + OD

Mà OA = OC, OB = OD

Suy ra: AB = CD

Vậy hình thang ACBD là hình thang cân.

Trường

Giải bài tập