Giải bài 3.1, 3.2, 3.3 trang 83, 84 SBT Toán 8 tập 1

Giải bài tập trang 83, 84 bài 3 hình thang cân Sách bài tập (SBT) Toán 8 tập 1. Câu 3.1: Hình thang cân ABCD (AB // CD) có…

Câu 3.1 trang 83 Sách bài tập (SBT) Toán lớp 8 tập 1

Hình thang cân ABCD (AB // CD) có (widehat A = {70^0}). Khẳng định nào dưới đây là đúng ?

A. (widehat C = {110^0})

Bạn đang xem: Giải bài 3.1, 3.2, 3.3 trang 83, 84 SBT Toán 8 tập 1

B. (widehat B = {110^0})

C. (widehat C = {70^0})

D. (widehat D = {70^0})

Giải:

Chọn A. (widehat C = {110^0})

Câu 3.2 trang 84 Sách bài tập (SBT) Toán lớp 8 tập 1

Hình thang cân ABCD (AB// CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy.

Giải:

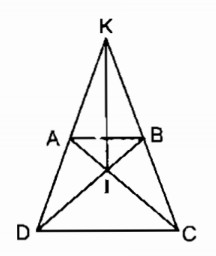
∆ACD = ∆BDC (c.c.c) suy ra  

do đó ID = IC           (1)

Tam giác KCD có hai góc ở đấy bằng nhau nên KD = KC          (2)

Từ (1) và (2) suy ra KI là đương trung trực của CD.

Chứng minh tương tự có IA = IB, KA = KB

Suy ra KI là đường trung trực của AB

Câu 3.3 trang 84 Sách bài tập (SBT) Toán 8 tập 1

Hình thang cân ABCD (AB // CD) có  , DB là tia phân giác của góc D. Tính các cạnh của hình thang, biết chu vi hình thang bằng 20cm.

Giải:

Hình thang ABCD cân có AB // CD

( Rightarrow widehat D = widehat C = {60^0})

DB là tia phân giác của góc D

( Rightarrow widehat {ADB} = widehat {BDC})

(widehat {ABD} = widehat {BDC}) (hai góc so le trong)

Suy ra: (widehat {ADB} = widehat {ABD})  

⇒ ∆ ABD cân tại A  ⇒ AB = AD (1)

Từ B kẻ đường thẳng song song với AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = ED, AD= BE   (2)

(widehat {BEC} = widehat {ADC}) (đồng vị )

Suy ra:  (widehat {BEC} = widehat C = {60^0})

⇒∆ BEC đều ⇒ EC = BC    (3)

AD = BC (tính chất hình thang cân)   (4)

Từ (1), (2), (3) và (4) ⇒ AB = BC = AD = ED = EC

⇒ Chu vi hình thang bằng:

AB + BC + CD + AD = AB + BC + EC +ED +AD = 5AB

⇒AB = BC = AD = 20:5 = 4 (cm)

CD = CE + DE = 2 AB = 2.4 = 8 (cm)

Trường

Giải bài tập