Giải bài tập trang 123 bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g) Sách giáo khoa (SGK) Toán 7. Câu 33: Vẽ tam giác ABC biết AC…
Bài 33 trang 123 – Sách giáo khoa toán 7 tập 1
Vẽ tam giác ABC biết AC=2cm, (widehat{A})= 900 (widehat{C}) = 600
Giải:
Bạn đang xem: Giải bài 33, 34, 35, 36 trang 123 SGK Toán 7
Cách vẽ:
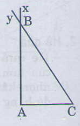
– Vẽ đoạn AC=2cm,
– Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho (widehat{CAx})= 900,
(widehat{ACy})=600
Hai tia cắt nhau ở B. tạo thành tam giác ABC cần vẽ.
Bài 34 trang 123 – Sách giáo khoa toán 7 tập 1
Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?

Giải:
Xem hình 98)
(∆ABC) và (∆ABD) có:
+) (widehat{CAB})=(widehat{DAB}) (gt)
=) (AB) là cạnh chung.
+) (widehat{ABC})=(widehat{ABD})(gt)
Suy ra (∆ABC=∆ABD) (g.c.g)
Xem hình 99)
Ta có:
(widehat{B_{1}})+(widehat{B_{2}}=180^0) (Hai góc kề bù).
(widehat{C _{1}})+ (widehat{C _{2}}=180^0) (Hai góc kề bù)
Mà (widehat{B_{2}})=(widehat{C _{2}}) (gt) nên (widehat{B_{1}})=(widehat{C _{1}})
* (∆ABD) và (∆ACE) có:
+) (widehat{B_{1}})=(widehat{C _{1}}) (cmt)
+) (BD=EC) (gt)
+) (widehat{D }) = (widehat{E }) (gt)
Suy ra (∆ABD=∆ACE) (g.c.g)
(DC=DB+BC)
(EB=EC+CB)
Do đó: (DC=EB)
* (∆ADC) và (∆AEB) có:
+) (widehat{D })=(widehat{E }) (gt)
+) (widehat{C _{2}})=(widehat{B_{2}}) (gt)
+) (DC=EB) (cmt)
Suy ra (∆ADC=∆AEB) (g.c.g)
Bài 35 trang 123 – Sách giáo khoa toán 7 tập 1
Cho góc (xOy) khác góc bẹt, (Ot) là tia phân giác của góc đó. Qua (H) thuộc tia (Ot) , kẻ đường vuông góc với (Ot), nó cắt (Ox) và (Oy) theo thứ tự (A) và (B).
a) Chứng minh rằng (OA=OB).
b ) Lấy điểm (C) thuộc tia (Ot), chứng minh rằng (CA=CB) và (widehat{OAC })= (widehat{OBC }).
Giải

a) Xét (∆AOH) và (∆BOH) có:
+) (widehat{AOH}=widehat{BOH}) (vì (Ot) là phân giác)
+) (OH) là cạnh chung
+) (widehat {AHO} = widehat {BHO},,left( { = {{90}^0}} right))
Suy ra (∆AOH =∆BOH) ( g.c.g)
Suy ra (OA=OB) (hai cạnh tương ứng).
b) Xét (∆AOC) và (∆BOC) có:
+) (OA=OB) (cmt)
+) (widehat{AOC}=widehat{BOC}) (gt)
+) (OC) cạnh chung.
Suy ra (∆AOC= ∆BOC) (c.g.c)
Suy ra: (CA=CB) ( hai cạnh tương ứng)
(widehat{OAC }= widehat{OBC }) ( hai góc tương ứng).
Bài 36 trang 123 – Sách giáo khoa toán 7 tập 1
Trên hình 100 ta có OA=OB, OAC=OBD.
Chứng minh rằng AC=BD.

Giải:
Xét ∆OAC và ∆OBD, có:
(widehat{OAC})=(widehat{OBD})(gt)
OA=OB(gt)
(widehat{O}) chung.
Nên ∆OAC=∆OBD(g.c.g)
Suy ra: AC=BD
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





