Giải bài tập trang 18 bài 2 tỉ số lượng giác của góc nhọn Sách bài tập (SBT) Toán 9 tập 1. Câu 36: Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9) …
Câu 36. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
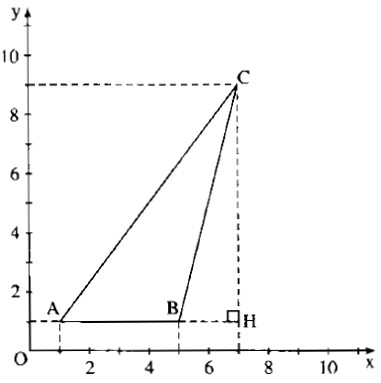
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9)
Bạn đang xem: Giải bài 36, 37, 38 trang 108 SBT Toán 9 tập 1
Hãy tính:
a) Giá trị của (tgwidehat {BAC}) (làm tròn đến chữ số thập phân thứ tư);
b) Độ dài của cạnh AC.
Gợi ý làm bài:
a) Vì tam giác ACH vuông tại H nên ta có:
(tgwidehat {HAC} = {{CH} over {AH}} = {{9 – 1} over {7 – 1}} = {8 over 6} = 1,3333)
Mà A, B, H thẳng hàng nên suy ra:
(tgwidehat {BAC} = tgwidehat {HAC} = 1,3333)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ACH, ta có:
(A{C^2} = C{H^2} + A{H^2})
Suy ra: (AC = sqrt {C{H^2} + A{H^2}} = sqrt {{8^2} + {6^2}} = sqrt {100} = 10)
Câu 37. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình 12.
Hãy viết một phương trình để từ đó có thể tìm được x (không phải giải phương trình này).

Gợi ý làm bài:

Từ đỉnh của góc 70°, kẻ đường cao của tam giác.
Sử dụng tỉ số sin của các góc, ta có phương trình: (xsin 30^circ = 4sin 80^circ )
Câu 38. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy tính sinL (làm tròn đến chữ số thập phân thứ tư), biết rằng (sin 30^circ = 0,5.)

Gợi ý làm bài:

Kẻ (MH bot NL)
Ta có: (sin 30^circ = {{MH} over {MN}} Rightarrow MH = sin 30^circ .MN = sin 30^circ .2,8)
(sin L = {{MH} over {ML}} = {{sin 30^circ .2,8} over {4,2}} = {{0,5.2,8} over {4,2}} = {1 over 3} approx 0,3333.)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





