Giải bài 37, 38, 39, 40 trang 124 SGK Toán 7

Giải bài tập trang 123, 124 bài 5 Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g) Sách giáo khoa (SGK) Toán 7. Câu 33: Trên mỗi hình 101,102,103 có tam giác nào bằng nhau…

Bài 37 trang 123 – Sách giáo khoa toán 7 tập 1

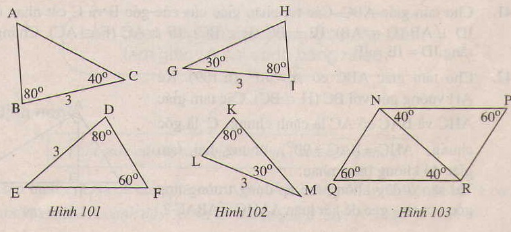
 Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?

Bạn đang xem: Giải bài 37, 38, 39, 40 trang 124 SGK Toán 7

Giải:

Tính các góc còn lại trên mỗi hình trên ta được:

Áp dụng định lí tổng ba góc trong một tam giác ta có:

(eqalign{
& widehat A = {180^0} – widehat B – widehat C = {180^0} – {80^0} – {40^0} = {60^0} cr
& widehat H = {180^0} – widehat G – widehat I = {180^0} – {30^0} – {80^0} = {70^0} cr
& widehat E = {180^0} – widehat D – widehat F = {180^0} – {80^0} – {60^0} = {40^0} cr
& widehat L = {180^0} – widehat K – widehat M = {180^0} – {80^0} – {30^0} = {70^0} cr
& widehat {QNR} = {180^0} – widehat {NRQ} – widehat {RQN} = {180^0} – {40^0} – {60^0} = {80^0} cr
& widehat {NRP} = {180^0} – widehat {RPN} – widehat {PNR} = {180^0} – {60^0} – {40^0} = {80^0} cr} )

– Xét (∆ABC) và (∆FDE) (Hình 101)

+) (widehat{B} = widehat{D})

+) (BC=DE)

+) (widehat{C}=widehat{E})

Suy ra (∆ABC=∆FDE)  (g.c.g)

– Xét  (∆NQR) và (∆RPN) (Hình 103)

+) (widehat{QNR}=widehat{NRP})  ((=80^0))

+) (NR) là cạnh chung.

+) (widehat{NRQ}=widehat{RNP})  ((40^0))

Suy ra (∆NQR=∆RPN)  (g.c.g)

– Xét (Delta HIG) và (Delta LKM) (Hình 102)

(eqalign{
& + ),,GI = ML cr 
& + ),,widehat G = widehat M cr 
& + ),,widehat I = widehat K cr} )

Ta có: (widehat G,; widehat I) cùng kề với cạnh (GI), còn (widehat M ) kề với cạnh (ML) nhưng ( widehat K) không kề với cạnh (ML) nên (Delta HIG) không bằng (Delta LKM).

 

---

Bài 38 trang 124 – Sách giáo khoa toán 7 tập 1

Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng 

AB=CD,AC=BD.

Giải.

Vẽ đoạn thẳng AD.

∆ADB và ∆DAC có:

 (widehat{A_{1}})= (widehat{D_{1}})(so le trong AB//CD)

AD là cạnh chung.

(widehat{A_{2}})=(widehat{D_{2}})(So le trong, AC//BD)

Do đó ∆ADB=∆DAC(g.c .g)

Suy ra: AB=CD, BD=AC

---

Bài 39 trang 124 – Sách giáo khoa toán 7 tập 1

Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?

Giải:

Hình 105

(∆ABH) và (∆ACH) có:

+) (BH=CH) (gt)

+) (widehat{AHB}=widehat{AHC}) (góc vuông)

+) (AH) là cạnh chung.

vậy (∆ABH=∆ACH) (c.g.c)

Hình 106

(∆DKE) và (∆DKF) có: 

+) (widehat{EDK}=widehat{FDK})(gt)

+) (DK) là cạnh chung.

+) (widehat{DKE}=widehat{DKF}) (góc vuông)

Vậy (∆DKE=∆DKF) (g.c.g)

Hình 107

Theo định lí tổng ba góc trong một tam giác ta có:

(eqalign{
& widehat {ABD} + widehat {BDA} + widehat {DAB} = {180^0} cr
& widehat {ACD} + widehat {CDA} + widehat {DAC} = {180^0} cr} )

Mặt khác ta có: 

(eqalign{
& widehat {DAB} = widehat {DAC},,,(gt) cr
& widehat {ABD} = widehat {ACD} = {90^0} cr} )

Nên (widehat {BDA} = widehat {CDA})

Xét (∆ABD) và (∆ACD) có:

+) (widehat {DAB} = widehat {DAC},,,(gt))

+) (AD) cạnh chung

+) (widehat {BDA} = widehat {CDA}) (cmt)

(∆ABD=∆ACD) (g.c.g)

Hình 108

Theo định lí tổng ba góc trong một tam giác ta có:

(eqalign{
& widehat {ABD} + widehat {BDA} + widehat {DAB} = {180^0} cr 
& widehat {ACD} + widehat {CDA} + widehat {DAC} = {180^0} cr} )

Mặt khác ta có: 

(eqalign{
& widehat {DAB} = widehat {DAC},,,(gt) cr 
& widehat {ABD} = widehat {ACD} = {90^0} cr} )

Nên (widehat {BDA} = widehat {CDA})

Xét (∆ABD) và (∆ACD) có:

+) (widehat {DAB} = widehat {DAC},,,(gt))

+) (AD) cạnh chung

+) (widehat {BDA} = widehat {CDA}) (cmt)

(∆ABD=∆ACD) (g.c.g)

 Suy ra: (BD=CD) (hai cạnh tương ứng )

             (AB=AC) (hai cạnh tương ứng )

Xét (∆DBE) và (∆DCH) 

+) ( widehat {EBD} = widehat {HCD} = {90^0} ) 

+) (BD=CD) (cmt)

+) (widehat {BDE} = widehat {CDH}) (đối đỉnh)

(∆DBE=∆DCH) (g.c.g)

Xét  (∆ABH)  và (∆ACE ) 

+) (widehat A) chung

+) (AB=AC) (cmt)

+) (widehat {ABH} = widehat {ACE} = {90^0})

(∆ABH=∆ACE ) (g.c.g)

 

---

Bài 40 trang 124 – Sách giáo khoa toán 7 tập 1

Cho tam giác ABC(AB≠AC), tia Ax đi qua trung điểm M của BC. 

Kẻ BE và CF vuông góc với Ax(E  ∈ Ax, F∈Ax ). So sánh độ dài BE và CF/

Giải

Hai tam giác vuông BME, CMF có:

BM=MC(gt)

(widehat{BME})=(widehat{CMF})(đối đỉnh)

 Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).

Suy ra BE=CF.

Trường

Giải bài tập