Giải bài tập trang 117 bài 4 một số hệ thức về cạnh và góc trong tam giác vuông Sách bài tập (SBT) Toán 9 tập 1. Câu 4.6: Trong hình thang ABCD, tổng của hai đáy AD và BC bằng b, đường chéo AC bằng a, góc ACB bằng α…
Câu 4.6 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Trong hình thang ABCD, tổng của hai đáy AD và BC bằng b, đường chéo AC bằng a, góc ACB bằng α. Hãy tìm diện tích của hình thang đó.
Gợi ý làm bài
Bạn đang xem: Giải bài 4.5, 4.6, 4.7, 4.8 trang 117 SBT Toán 9 tập 1
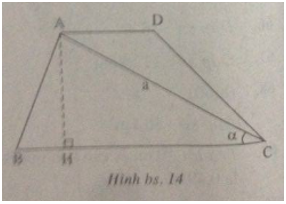
Kẻ đường cao AH của tam giác ABC (h.bs.14). Ta có AD + BC = b, AC = a, (widehat {ACB} = alpha ), suy ra:
AH = asinα và diện tích hình thang là:
(S = {{AD + BC} over 2}.AH = {{ab} over 2}sin alpha .)
Câu 4.5 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy tìm diện tích của tam giác cân có góc ở đáy bằng α nếu biết:
a) Cạnh bên bằng b ;
b) Cạnh đáy bằng a.
Gợi ý làm bài

Xét tam giác cân ABC có AB = AC, (widehat {ABC} = alpha ) đường cao AH (h.bs.13).
a) AB = AC = b thì AH = bsinα, BH = bcosα nên diện tích tam giác ABC là
(eqalign{
& S = {1 over 2}AH.BC = AH.BH cr
& = {b^2}sin alpha cos alpha . cr} )
b) BC = a thì (AH = {a over 2}tgalpha )
nên (S = {a over 2}.AH = {{{a^2}} over 4}tgalpha ).
Câu 4.7 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC có BC = 7, (widehat {ABC} = 42^circ ,widehat {ACB} = 35^circ .) Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH ( làm tròn kết quả đến chữ số thập phân thứ ba).
Gợi ý làm bài

(h.bs. 15). Đặt AH = h thì rõ ràng:
(eqalign{
& BH = hcot gwidehat {ABH} = hcot g42^circ , cr
& CH = hcot gwidehat {ACH} = hcot g35^circ cr} )
(để ý rằng H thuộc đoạn BC vì 35º, 42 º đều là góc nhọn). Do đó
7 = BC = BH + CH = h (cotg42 º + cotg35 º), suy ra
(eqalign{
& h = {7 over {cot g42 + cot g35}} cr
& = {7 over {tg48 + tg55}} approx 2,757. cr} )
Câu 4.8 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đó kẻ từ M. Chứng minh rằng:
a) ({S_{MNP}} = {1 over 2}MP.NP.sin P);
b) (DP = {{MN.sin N} over {tgP}});
c) ∆DNE đồng dạng với ∆MNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P.
Gợi ý làm bài

(h.bs. 16)
a) Ta có MD = MP sin P, suy ra:
({S_{MNP}} = {1 over 2}NP.MD = {1 over 2}NP.MPsin P.)
b) Ta có MD = MN sin N và MD = DP tg P nên từ đó suy ra DP ( = {{MNsin N} over {tgP}})
c) Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên ({{DN} over {MN}} = {{EN} over {PN}}.)
Hai tam giác DNE và MNP đồng dạng vì có góc N chung và ({{DN} over {MN}} = {{EN} over {PN}}.)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





