Giải bài 40, 41, 42 trang 142 SBT Toán lớp 7 tập 1

Giải bài tập trang 142 bài 4 trường hợp bằng nhau thứ nhất của tam giác cạnh-góc-cạnh (c-g-c) Sách Bài Tập Toán lớp 7 tập 1. Câu 40: Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB…

Câu 40 trang 142 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB.

Giải

Bạn đang xem: Giải bài 40, 41, 42 trang 142 SBT Toán lớp 7 tập 1

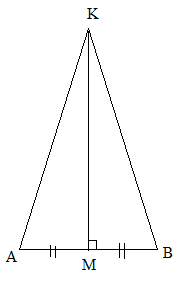
Xét ∆AMK và ∆BMK, ta có:

AM = BM (gt)

(widehat {AMK} = widehat {BMK} = 90^circ ) (vì (KM bot AB))

MK cạnh chung

Suy ra: ∆AMK = ∆BMK(c.g.c)

(Rightarrow widehat {AKM} = widehat {BKM})

Vậy KM là tia phân giác của (widehat {AKB}).

Câu 41 trang 142 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh rằng AC // BD.

Giải

Xét ∆AOC và ∆BOD, ta có:

OA = OB (gt)

(widehat {AOC} = widehat {BO{rm{D}}}) (đối đỉnh)

OC = OD (gt)

Suy ra:∆AOC = ∆BOD (c.g.c)

( Rightarrow widehat A = widehat B) (hai góc tương ứng)

Vậy: AC // BD (vì có hai góc ở vị trí so le trong bằng nhau)

Câu 42 trang 142 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có (widehat A = 90^circ ). Trên tia đối của tia CA lấy điểm D sao cho CD = CA, Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE.

Giải