Giải bài tập trang 128 bài ôn tập chương II SGK Toán 9 tập 1. Câu 41: Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H…
Bài 41 trang 128 SGK Toán 9 tập 1
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Bạn đang xem: Giải bài 41, 42, 43 trang 128 SGK Toán 9 tập 1
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O); (K) và(O); (I) và (K).
b) Tứ giác AEHF là hình gì? Vì sao?
c) Chứng minh đẳng thức (AE.AB = AF.AC)
d) Chứng minh rằng EF là tiếp tuyến chung của hai đường trong (I) và (K)
e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.
Hướng dẫn làm bài:
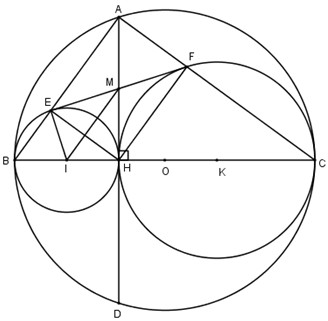
a) (OI = OB – IB) nên (I) tiếp xúc trong với (O)
(OK = OC – KC) nên (K) tiêó xúc trong với (O)
(IK = IH + KH) nên (I) tiếp xúc ngoài với (K)
b) (widehat {BEH} = 90°) (E thuộc đường tròn đường kính BH)
( Rightarrow widehat {A{rm{E}}H} = {90^0})
Tương tự có (widehat {AFH} = {90^0};widehat {BAC} = {90^0})
Tứ giác AEHF có (widehat {EAF} = widehat {AEH} = widehat {AFH} = {90^0}) nên là hình chữ nhật.
c) ∆ABH vuông tại H, HE là đường cao nên (AH^2 = AE. AB)
∆ACH vuông tại H, HF là đường cao nên (AH^2 = AF. AC)
Do đó (AE. AB = AF. AC)
d) Gọi M là giao điểm của AH và EF, ta có: (ME = MF = MH = MA)
Xét ∆MEI và ∆MHI có:
(ME = MH, IE = IH (=R)), MI (cạnh chung)
Do đó (∆MEI = ∆MHI) (c.c.c)
(Rightarrow widehat {MEI} = widehat {MHI})
mà (widehat {MHI} = {90^0}) nên (widehat {MEI} = {90^0})
⇒ EF là tiếp tuyến của đường tròn (I)
Chứng minh tương tự có EF là tiếp tuyến của đường tròn (K)
e) Ta có (EF = AH) mà (AH ≤ AO = R)
Do đó (EF ≤ R), không đổi. Dấu “=” xảy ra (⇔ H ≡ O)
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
Bài 42 trang 128 SGK Toán 9 tập 1
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài. B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng
a) Tứ giác AEMF là hình chữ nhật.
b) ME.MO = MF.MO’
c) OO’ là tiếp tuyến của đường tròn có đường kính là BC.
d) BC là tiếp tuyến của đường tròn có đường kính là OO’.
Hướng dẫn làm bài:

a) (MA, MB) là các tiếp tuyến của đường tròn (O) (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có (MA = MB), MO là tia phân giác (widehat {AMB})
(∆MAB) cân tại (M (MA = MB))
Có MO là đường phân giác nên đồng thời là đường cao
(Rightarrow MO bot AB Rightarrow widehat {ME{rm{A}}} = {90^0})
Chứng minh tương tự có MO’ là tia phân giác góc (widehat {AMC}) và (widehat {MFA} = 90^0)
(MO, MO’) là tia phân giác của hai góc kẻ bù (widehat {AMB},widehat {AMC} Rightarrow widehat {EMF} = {90^0})
Tứ giác AEMF là hình chữ nhật (vì (widehat {EMF} = widehat {MEA} = widehat {MFA} = {90^0})
b) (∆MAO) vuông tại A có AE là đường cao nên (ME. MO = MA^2)
Tương tự, ta có: (MF. MO’ = MA^2)
Do đó, (ME. MO = MF. MO’ (= MA^2))
c) Ta có (MA = MB = MC) nên M là tâm đường tròn đường kính BC có bán kính là MA. Mà (OO’ ⊥ MA) tại A.
Do đó OO’ là tiếp tuyến của đường tròn đường kính BC
d) Gọi K là trung điểm OO’, ta có K là tâm đường tròn có đướng kính là OO’, bán kính KM ((∆MOO’) vuông tại M)
Ta có (OB ⊥ BC, O’C ⊥ BC ⇒ OB // OC.)
Tứ giác OBCO’ là hình thang có K, M lần lượt là trung điểm các cạnh cạnh bên OO’, BC.
Do đó KM là đường trung bình của hình thang OBCO’ (⇒ KM // OB)
Mà (OB ⊥ BC) nên (KM ⊥ BC)
Ta có (BC ⊥ KM) tại M nên BC là tiếp tuyến của đường tròn đường kính OO’
Bài 43 trang 128 SGK Toán 9 tập 1
Cho hai đường tròn(O; R) và (O’; r) cắt nhau tại A và (B (R > r)). Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt cá đường tròn tâm (O; R) và (O’; r) theo thứ tự tại C và D (khác A).
a) Chứng minh rằng AC = AD.
b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB
Hướng dẫn làm bài:

a) Vẽ OM ⊥ CD tại M, O’N ⊥CD tại N, ta có:
(MA = MC = {{AC} over 2};)
(NA = N{rm{D}} = {{A{rm{D}}} over 2})
Mặt khác, ta có (OM ⊥ CD, IA ⊥ CD, O’N ⊥ CD)
(⇒ OM // IA //O’N.)
Hình thang OMNO’ (OM //O’N) có (IA // OM; IO = IO’) nên (MA = NA.) Do vậy (AC = AD)
b) (O) và (O’) cắt nhau tại A, B
⇒ OO’ là đường trung trực của đoạn thẳng AB
(⇒ IA = IB)
Mặt khác (IA = IK) ( vì K đối xứng với A qua I)
Do đó: (IA = IB = IK)
Ta có ∆KBA có BI là đường trung tuyến và (BI = {{AK} over 2}) nên ∆KBA vuông tại B
(⇒ KB ⊥ AB)
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





