Giải bài tập trang 86 bài 5 dựng hình bằng thước và com pa. Dựng hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 53: Dựng hình thang cân ABCD(AB // CD), biết AD = 2cm, CD = 4cm, AC = 3,5cm…
Câu 53 trang 86 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình thang cân ABCD(AB // CD), biết AD = 2cm, CD = 4cm, AC = 3,5cm.
Giải:
Bạn đang xem: Giải bài 53, 54, 55, 56 trang 86 SBT Toán 8 tập 1
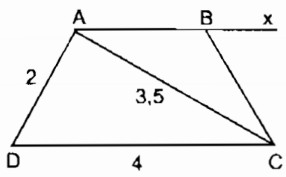
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADC dựng được vì biết ba cạnh AD = 2cm, CD = 4cm, AC = 3,5cm. Điểm B thỏa mãn 2 điều kiện:
– B nằm trên đường thẳng đi qua A và song song với CD
– B cách D một khoảng bằng 3,5 cm
Cách dựng:
– Dựng tam giác ADC biết AD = 2cm, AC = 3,5 cm, CD = 4cm
– Dựng tia Ax // CD, Ax nằm trong nửa mặt phẳng bờ AD chứa điểm C
– Dựng cung tròn tâm D bán kính 3,5cm. Cung này cắt Ax tại B. Nối CB ta có hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB // CD.
AC = BD = 3,5 cm
Vậy hình thang ABCD là hình thang cân.
Hình thang cân ABCD có: AD = 2cm, CD = 4cm, AC = 3,5cm thỏa mãn yêu cầu bài toán.
Biện luận: Tam giác ADC luôn dựng được nên hình thang ABCD luôn dựng được. Cung tròn tâm D bán kính 3,5cm cắt Ax tại 1 điểm ta dựng được một hình thang thỏa mãn yêu cầu bài toán.
Câu 54 trang 86 Sách bài tập(SBT) Toán 8 tập 1
Dựng hình thang cân ABCD(AB // CD), biết hai đáy AB = 2cm, CD = 4cm, đường cao AH = 2cm.
Giải:

Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADH dựng được vì biết hai cạnh góc vuông AH = 2cm và HD = 1cm, (widehat H = {90^0}). Vì đáy AB
Điểm C nằm trên tia đối tia HD và cách H
Điểm B thỏa mãn hai điều kiện:
– B nằm trên đường thẳng đi qua A và song song với DH.
– B cách A một khoảng bằng 2cm
Cách dựng:
– Dựng ∆ AHD biết (widehat H = 1V), AH =2cm, HD = 1cm
– Dựng tia đối tia HD
– Dựng điểm C sao cho HC = 3cm
– Dựng tia Ax // DH, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm H
– Dựng điểm B sao cho AB = 2cm. Nối CB ta có hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB // CD
Kẻ BK ⊥ CD. Tứ giác ABKH là hình thang có hai cạnh bên song song
Nên : BK = AH và KH = AB
Suy ra: KC = HC – KH = HC – AB = 3− 2 = 1 (cm)
Suy ra: ∆ AHD = ∆ BKC (c.g.c) (Rightarrow widehat D = widehat C)
Vậy hình thang ABCD là hình thang cân.
Hình thang cân ABCD có: AH = 2cm, đáy AB = 2cm, đáy CD = 4cm
Thỏa mãn điều kiện bài toán.
Biện luận: Tam giác AHD luôn dựng được nên hình thang ABCD luôn dựng được. Ta luôn dựng được một hình thang thỏa mãn điều kiện bài toán.
Câu 55 trang 86 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình thang ABCD, biết hai đáy AB = 2cm, CD = 4cm, (widehat C = {50^0},widehat D = {70^0}).
Giải:

Phân tích: Giả sử hình thang ABCD thỏa mãn yêu cầu bài toán. Qua A kẻ đường thẳng song song với BC cắt CD tại E. Hình thang ABCE có hai cạnh bên song song nên AB = EC = 2cm do đó DE = 2cm
Tam giác ADE dựng được vì biết 2 góc kề với một cạnh.
Điểm C nằm trên tia DE cách D một khoảng bằng 4cm
Điểm B thỏa mãn hai điều kiện:
– B nằm trên đường thẳng đi qua A và song song với CD.
– B nằm trên đường thẳng đi qua C và song song với AE.
Cách dựng:
– Dựng tam giác ADE biết DE = 2cm, (widehat D = {70^0},widehat E = {50^0})
– Dựng tia DE lấy điểm C sao cho DC = 4cm
– Dựng tia Ax // CD, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm C
– Dựng tia Cy // AE, Cy nằm trên nửa mặt phẳng bờ CD chứa điểm A. Cy cắt Ax tại B. Hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB // CD
CD = CE + ED ⇒ CE = CD – ED = 4 – 2 =2 (cm)
Hình thang ABCE có hai cạnh bên AE // CB
⇒ AB = CE = 2 (cm)
(widehat C = widehat E = {50^0}) (hai góc đồng vị)
(widehat D = {70^0})
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADE luôn dựng được, hình thang ABCD luôn dựng được. Ta dựng được một hình thang thỏa mãn điều kiện bài toán.
Câu 56 trang 86 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình thang ABCD, biết hai đáy AB = 1cm, CD = 4cm, hai cạnh bên AD = 2cm, BC = 3cm.
Giải:

Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Qua A kẻ đường thẳng song song với BC cắt CD tại E ta thấy tam giác AED xác định vì biết ba cạnh, ta cần xác định đỉnh B và C
– Đỉnh C nằm trên tia DE, cách D một khoảng bẳng 4cm
– Đỉnh B nằm trên đường thẳng đi qua A song song với đường thẳng DE và cách A một khoảng bằng 1cm.
Cách dựng:
– Dựng ∆ ADE biết AD = 2cm, DE = 3cm, AE = 3cm
– Trên tia DE dựng điểm C sao cho DC = 4cm
– Dựng đường thẳng đi qua A và song song với DC, lấy điểm B sao cho AB = 1cm. Nối BC ta có hình thang ABCD cần dựng
Chứng minh: Thật vậy theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang.
Ta có: AD = 2cm, DC = 4cm, AB = 1cm, hình thang ABCE có hai cạnh đáy AB = EC = 1cm nên BC = AE = 3cm.
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADE luôn dựng được nên hình thang ABCD dựng được, bài toán có một nghiệm hình.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





