Giải bài tập trang 114 bài 4 một số hệ thức về cạnh và góc trong tam giác vuông Sách bài tập (SBT) Toán 9 tập 1. Câu 56: Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới gốc 30° so với đường nằm ngang chân đèn…
Câu 56. Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
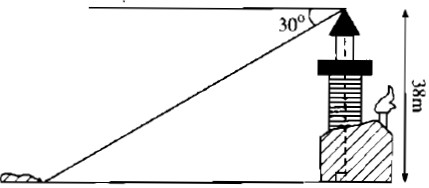
Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới gốc 30° so với đường nằm ngang chân đèn. Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?
Bạn đang xem: Giải bài 56, 57, 58, 59 trang 114 SBT Toán 9 tập 1
Gợi ý làm bài:
Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30° , chiều cao của cột đèn biển là cạnh đối diện với góc 30° .
Vậy khoảng cách từ đảo đến chân đèn là:
(38.cot g30^circ approx 65,818left( {cm} right))
Câu 57.trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
Trong tam giác ABC có (AB = 11cm,widehat {ABC} = 38^circ ,widehat {ACB} = 30^circ ). N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC.

Gợi ý làm bài:
Trong tam giác vuông ABN, ta có:
(AN = AB.sin widehat B = 11.sin 38^circ approx 6,772left( {cm} right))
Trong tam giác vuông ACN, ta có:
(AC = {{AN} over {sin widehat C}} approx {{6,772} over {sin 30^circ }} = 13,544left( {cm} right))
Câu 58.trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
Để nhìn thấy đỉnh A của một vách đá dựng đứng, người ta đã đứng tại điểm P cách chân vách đá một khoảng 45m và nhìn lên một góc 25° so với đường nằm ngang (góc nhìn lên này được gọi là góc “nâng”). Hãy tính độ cao của vách đá.

Gợi ý làm bài:
Chiều cao vách đá là cạnh góc vuông đối diện với góc 25° . Khi đó chiều cao của vách đá là:
(45.tg25^circ approx 20,984left( m right))
Câu 59. Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
Tìm x và y trong các hình sau:
Gợi ý làm bài:
a) Hình a

Trong tam giác vuông ACP,ta có:
(x = CP = AC.sin widehat A)
( = 8.sin 30^circ = 8.{1 over 2} = 4)
Trong tam giác vuông BCP, ta có:
(y = BC = {x over {cos widehat {BCP}}} = {4 over {{rm{cos50}}^circ }} approx 6,223)
b) Hình b

Trong tam giác vuông ABC, ta có:
(x = AC = BC.sin widehat B)
( = 7.sin 40^circ approx 4,5)
Trong tam giác vuông ACD, ta có:
(y = AD = AC.cot gwidehat D)
( approx 4,5cot g60^circ = 2,598)
c) Hình c

Vì tứ giác CDPQ có hai góc vuông và hai cạnh CD = DP = 4 nên nó là hình vuông. Suy ra: CD = DP = PQ = QC = 4
Trong tam giác vuông BCQ, ta có:
(x = BC = {{CQ} over {{rm{cos}}widehat {BCQ}}} = {4 over {{rm{cos50}}^circ }} approx 6,223)
(BQ = BC.sin widehat {BCQ} approx 6,223.sin 50^circ = 4,767)
Trong tam giác vuông ADP, ta có:
(AP = DP.cot gA = 4.cot g70^circ approx 1,456)
Ta có:
(y = AB = AP + PQ + QB)
(= 1,456 + 4 + 4,767 = 10,223).
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





