Giải bài 57, 58, 59, 60 trang 145 SBT Toán lớp 7 tập 1

Giải bài tập trang 145 bài 5 trường hợp bằng nhau thứ nhất của tam giác góc-cạnh-góc (g-c-g) Sách Bài Tập Toán lớp 7 tập 1. Câu 57: Cho hình dưới trong đó DE // AB, DF // AC, EF // BC. Tính chu vi tam giác DFE….

Câu 57 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho hình dưới trong đó DE // AB, DF // AC, EF // BC. Tính chu vi tam giác DFE.

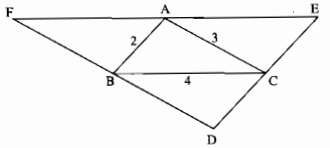
Bạn đang xem: Giải bài 57, 58, 59, 60 trang 145 SBT Toán lớp 7 tập 1

Giải

Xét ∆ABC và ∆ ABF, ta có:

(widehat {ABC} = widehat {{rm{BAF}}}) (so le trong)

AB cạnh chung

(widehat {BAC} = widehat {ABF}) (so le trong)

Suy ra: ∆ABC =  ∆ ABF (g.c.g)

Suy ra: AF = BC = 4 (2 cạnh tương ứng)

              BF = AC = 3 (2 cạnh tương ứng)

Xét ∆ABC và ∆ACE, ta có:

(widehat {ACB} = widehat {CA{rm{E}}}) (so le trong)

AC cạnh chung 

(widehat {BAC} = widehat {EC{rm{A}}}) (so le trong)

Suy ra: ∆ABC  =  ∆CEA (g.c.g)

Suy ra: AE = BC = 4 (2 cạnh tương ứng)

             CE = AB = 2 (2 cạnh tương ứng)

Xét ∆ABC và ∆DCB, ta có:

(widehat {ACB} = widehat {DBC}) (so le trong)

BC cạnh chung

(widehat {ABC} = widehat {DCB}) (so le trong)

Suy ra: ∆ABC =  ∆DCB (g.c.g)

Suy ra: DC = AB = 2 (2 cạnh tương ứng)

              DB = AC = 3 (2 cạnh tương ứng)

Ta có:   EF = AE + AF = 4 + 4 = 8

              DF = DB + BF = 3 + 3 = 6

              DE = DC + CE = 2 + 2 = 4

Vậy chu vi ∆DEF là:

DE + DF + EF = 4 + 6 + 8 = 18 (đơn vị độ dài)

Câu 58 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho đoạn thẳng AB. Qua A vẽ đường thẳng m vuông góc với AB. Qua B vẽ đường thẳng n vuông góc với AB. Qua trung điểm O của AB vẽ một đường thẳng cắt m ở C và cắt n ở D. So sánh các độ dài OC và OD.

 Giải

Xét ∆AOC = ∆BOD, ta có:

(widehat {CAO} = widehat {DBO} = 90^circ ) (gt)

OA = OB (gt)

(widehat {AOC} = widehat {BO{rm{D}}}) (đối đỉnh)

Suy ra: ∆AOC = ∆BOD (g.c.g)

Vậy OC = OD (2 cạnh tương ứng)

Câu 59 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có AB = 2,5cm, AC = 3cm, BC = 3,5cm. Qua A vẽ đường thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau ở D. Tính chu vi tam giác ACD.

Giải

Ta có: AB // CD (gt)

Suy ra: (widehat {AC{rm{D}}} = widehat {CAB}) (2 góc so le trong)

              BC // AD (gt)

Suy ra: (widehat {{rm{CAD}}} = widehat {ACB}) (2 góc so le trong)

Xét ∆ABC = ∆CDA, ta có:

(widehat {AC{rm{D}}} = widehat {CAB}) (chứng minh trên)

AC cạnh chung

(widehat {CA{rm{D}}} = widehat {ACB}) (chứng minh trên)

Suy ra:  ∆ABC = ∆CDA (g.c.g)

Suy ra: CD = AB = 2,5(cm) và AD = BC = 3,5 (cm)

Chu vi ∆ACD là: AC + AD + CD = 3 + 3,5 + 2,5 = 9 (cm)

Câu 60 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. Kẻ DE vuông góc với BC. Chứng minh rằng AB = BE.

Giải

Xét hai tam giác vuông ABD và EBD, ta có:

(widehat {BA{rm{D}}} = widehat {BE{rm{D}}} = 90^circ )

Cạnh huyền BD chung

(widehat {AB{rm{D}}} = widehat {EB{rm{D}}}left( {gt} right))

Suy ra: ∆ABD = ∆EBD (cạnh huyền góc nhọn)

Vậy BA = BE (hai cạnh tương ứng) 

Trường

Giải bài tập