Giải bài tập trang 87, 88 bài Ôn tập chương III – Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác Sách giáo khoa (SGK) Toán 7. Câu 67: Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q….
Bài 67 trang 87 sgk toán 7 tập 2
Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q.
a)Tính tỉ số các diện tích của hai tam giác MPQ và RPQ.
Bạn đang xem: Giải bài 67, 68, 69, 70 trang 87, 88 SGK Toán 7
b)Tính tỉ số các diện tích của hai tam giác MNQ và RNQ.
Tức các kết quả trên, hãy chứng minh các tam giác QMN, QNP, QPM có cùng diện tích.
Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung đườn cao.
Hướng dẫn làm bài:
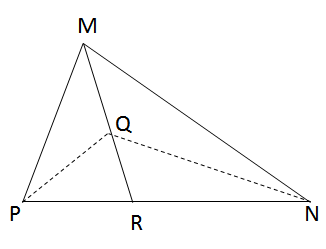
a) Vì Q là trọng tâm của ∆MNP nên điểm Q thuộc đường trung tuyến MR và ({{MQ} over {RQ}} = 2).
Vì hai tam giác ∆MPQ và ∆RPQ có chung đường cao kẻ từ P nên :
({{{S_{Delta MPQ}}} over {{S_{Delta RPQ}}}} = {{MQ} over {RQ}} = 2) (1)
b) Chứng minh tương tự như câu (a) ta có :
({{{S_{Delta MPQ}}} over {{S_{Delta RPQ}}}} = 2left( 2 right))
c) Hai tam giác ∆PQR và ∆QNR có chung đường cao kẻ từ Q và PR = RN nên S∆PQR = S∆QNR
Vì S∆PQR + S∆QNR = S∆PQN
Nên S∆PQN = 2.S∆PQR = 2.S∆QNR (3)
Từ (1), (2), (3) => S∆QMN = S∆QNP = S∆QPM
Bài 68 trang 88 sgk toán 7 tập 2
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy.
a) Hãy tìm điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B.
b) Nếu OA = OB thì có bao nhieu điểm M thỏa mãn các điều kiện trong câu a?
Hướng dẫn làm bài:

a) Vì M cách đều hai cạnh Ox, Oy của (widehat {xOy}) nên M phải thuộc tia phân giác (widehat {xOy}).
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác (widehat {xOy}) và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác (widehat {xOy}) cũng là trung trực của AB nên mọi điểm trên tia phân giác (widehat {xOy}) sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác (widehat {xOy}) đều thỏa mãn các điều kiện ở câu a.
Bài 69 trang 88 sgk toán 7 tập 2
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Hướng dẫn làm bài:

(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Bài 70 trang 88 sgk toán 7 tập 2
Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.
a) Ta kí hiệu PA là nửa mặt phẳng bờ d có chứa điểm A (không kể đường thẳng d). Gọi N là một điểm của PA và N là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA
b) Ta kí hiệu PB là nửa mặt phẳng bờ d có chứa điểm B (không kể điểm d). Gọi N’ là một điểm của PB. Chứng minh rằng N’B
c) Gọi L là một điểm sao cho LA A, PB hay trên d?
Hướng dẫn làm bài:

a) Vì M nằm trên d, d là trung trực của AB nên MA = MB (1)
Vì nên đoạn thẳng NB cắt d tại M suy ra M nằm giữa N và B.
Hay NM + MB = NB (2)
Từ (1) và (2) => NB = MA + NM
b) Gọi AN’ cắt d tại I
Trong tam giác N’IB có : N’B
Mà IA = IB (I thuộc trung trực của AB)
=> N’B N’B
c) Vì LA A.
Trường
Đăng bởi: Thcs-thptlongphu.edu.vn
Chuyên mục: Tổng hợp





