Giải bài 73, 74, 75, 76 trang 89 SBT Toán 8 tập 1

Giải bài tập trang 89 bài 7 hình bình hành Sách bài tập (SBT) Toán 8 tập 1. Câu 73: Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không…

Câu 73 trang 89 Sách bài tập (SBT) Toán 8 tập 1

Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?

 Giải:                                                                                 

Bạn đang xem: Giải bài 73, 74, 75, 76 trang 89 SBT Toán 8 tập 1

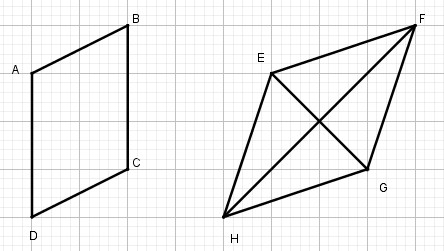
Tứ giác ABCD là hình bình hành vì có cạnh đối AD // BC và AD = BC bằng 3 cạnh ô vuông.

Tứ giác EFGH là hình bình hành vì có các cạnh đối bằng nhau.

EH = FG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông

EF = HG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông.

Câu 74 trang 89 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng DE = BF.

Giải:                                                                      

Ta có: AB = CD ( tính chất hình bình hành)

 (eqalign{  & EB = {1 over 2}AB(gt)  cr  & FD = {1 over 2}CD(gt) cr} )

Suy ra: EB = FB  (1)

Mà AB // CD (gt)

⇒ BE // FD   (2)

Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE = BF (tính chất hình bình hành)

Câu 75 trang 89 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.

Giải:                                                                            

Ta có:  (widehat A = widehat C)  (tính chất hình bình hành)

(eqalign{  & {widehat A_2} = {1 over 2}widehat A(gt)  cr  & {widehat C_2} = {1 over 2}widehat C(gt) cr} )

Suy ra:  

              AB // CD (gt)

hay AN // CM (1)

Mà  ({widehat N_1} = {widehat C_2}) (so le trong)

Suy ra: ({widehat A_2} = {widehat N_1})

⇒ AM // CN ( vì có các cặp góc ở vị trí đồng vị bằng nhau) (2)

Từ (1) và (2) suy ra: Tứ giác AMCN là hình bình hành ( theo định nghĩa)

Câu 76 trang 89 Sách bài tập (SBT) Toán 8 tập 1

Trên hình 8, cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.

Giải:                                                                

Gọi O là giao điểm của AC và BD

OA = OC ( tính chất hình bình hành) (1)

Xét hai tam giác vuông AEO và CFO, ta có:

(widehat {AEO} = widehat {CFO} = {90^0})

OA = OC ( chứng minh trên)

(widehat {AOE} = widehat {COF}) (đối đỉnh)

Do đó ∆ AEO =∆ CFO ( cạnh huyền, góc nhọn)

⇒ OE = OF (2)

Từ (1) và (2) suy ra tứ giác AECF là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Trường

Giải bài tập