Giải bài 88, 89, 90, 91 trang 90, 91 SBT Toán 8 tập 1

Giải bài tập trang 90, 91 bài 7 hình bình hành Sách bài tập (SBT) Toán 8 tập 1. Câu 88: Cho tam giác ABC. Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE…

Câu 88 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC. Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng:

a. IA = BC;                                       b. IA ⊥ BC.

Bạn đang xem: Giải bài 88, 89, 90, 91 trang 90, 91 SBT Toán 8 tập 1

Giải:    

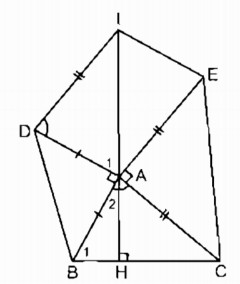
a. (widehat {BAC} + widehat {BAD} + widehat {DAE} + widehat {EAC} = {360^0})

    (widehat {BAD} = {90^0},widehat {EAC} = {90^0}(gt))

Suy ra: (widehat {BAC} + widehat {DAE} = {180^0}) (1)

            AE // DI (gt)

⇒ (widehat {ADI} + widehat {DAE} = {180^0}) (hai góc trong cùng phía) (2)

Từ (1) và (2) suy ra:  

Xét ∆ ABC và ∆ DAI :

AB = AD (gt)

(widehat {BAC} = widehat {ADI}) (chứng minh trên)

AC = DI (vì cùng bằng AE)

Do đó: ∆ ABC = ∆ DAI (c.g.c) ⇒ IA = BC

b. ∆ ABC = ∆ DAI ( chứng minh trên) ( Rightarrow {widehat A_1} = {widehat B_1})  (3)

Gọi giao điểm IA và BC là H.

Ta có: ({widehat A_1} + widehat {BAD} + {widehat A_2} = {180^0}) (kề bù)

mà (widehat {BAD} = {90^0}(gt) Rightarrow {widehat A_1} + {widehat A_2} = {90^0}) (4)

Từ (3) và (4) suy ra: ({widehat B_1} = {widehat A_2} = {90^0})

Trong ∆ AHB ta có: (widehat {AHB} + widehat {{B_1}} + {widehat A_2} = {180^0})

Suy ra (widehat {AHB} = {90^0} Rightarrow AH bot BC) hay IA ⊥ BC

Câu 89 trang 91 Sách bài tập (SBT) Toán 8 tập 1

Dựng hình bình hành ABCD, biết:                                         

a. AB = 2cm, AD = 3cm, (widehat A = {110^0})

b. AC = 4cm, BD = 5cm, (widehat {BOC} = {50^0}) (O là giao điểm của hai đường chéo).

Giải:                                                      

Cách dựng:

Dựng ∆ ABD có AB = 2cm, (widehat A = {110^0}), AD = 3cm

–  Dựng tia Bx // AD

–  Dựng tia Dy // AB cắt Bx tại C

Ta có hình bình hành ABCD cần dựng

Chứng minh: AB // CD, AD // BC nên tứ giác ABCD là hình bình hành.

Ta lại có AB = 2cm, (widehat A = {110^0}) , AD = 3cm. Bài toán có một nghiệm hình.

b.

Cách dựng:

–  Dựng ∆ OBC có OC = 2cm, OB = 2,5cm , (widehat O = {50^0})

–  Trên tia đối tia OC lấy điểm A sao cho OA = OC = 2cm

–  Trên tia đối tia OB lấy điểm D sao cho AD = OB = 2,5cm

Nối AB, BC, CD, AD ta có hình bình hành ABCD cần dựng

Chứng minh: Tứ giác ABCD có OA = OC, OB = OD nên nó là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.

Có AC = 4cm, BD = 5cm, (widehat {BOC} = {50^0})

Bài toán có một nghiệm hình.

Câu 90 trang 91 Sách bài tập (SBT) Toán 8 tập 1

Cho ba điểm A, B, C trên giấy kẻ ô vuông (h.12). Hãy vẽ điểm thứ tư M sao cho A, B, C, M là bốn đỉnh của một hình bình hành

Giải:                                                               

       –            Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có cạnh là hai ô vuông nên (C{M_1}) là đường chéo hình vuông cạnh 2 ô vuông và A, ({M_1})nằm trên nửa mặt phẳng bờ BC ta có hình bình hành (ABC{M_1}) .

       –            Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông , điểm B cách ({M_2}) là ba ô vuông và C, ({M_2})cũng nằm trên nửa mặt phẳng bờ AB ta có hình bình hành (AB{M_2}C)

       –            Nếu hình bình hành nhận AB làm đường chéo thì điểm ({M_3}) cách điểm B ba ô vuông, ({M_3})và A nằm trên cũng một nửa mặt phẳng bờ BC ta có hình bình hành (ACB{M_3}) .

Câu 91 trang 91 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC. Dựng đường thẳng song song với BC, cắt cạnh AB ở E, cắt cạnh AC ở F sao cho BE = AF.

Giải:                                                               

Cách dựng:

       –            Dựng đường phân giác AD

       –            Qua D dựng đường thẳng song song AB cắt AC tại F.

       –            Qua F dựng đường thẳng song song với BC cắt AB tại E.

Ta có điểm E, F cần dựng.

Chứng minh: DF // AB

( Rightarrow {widehat A_1} = {widehat D_1}) (so le trong)

     ({widehat A_1} = {widehat A_2}) (gt)

Suy ra: ({widehat D_1} = {widehat A_2})

⇒ ∆ AFD cân tại F

⇒ AF = DF (1)

    DF // AB hay DF // BE

    EF // BC hay EF // ED

Tứ giác BDFE là hình bình hành ⇒ BE = DF (2)

Từ (1) và (2) suy ra: AF = BE

Trường

Giải bài tập