Giải bài 9, 10, 11, 12 trang 138 SBT Toán lớp 7 tập 1

Giải bài tập trang 138 bài 1 tổng ba góc của một tam giác Sách Bài Tập Toán lớp 7 tập 1. Câu 9: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Tìm góc bằng góc B….

Câu 9 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Tìm góc bằng góc B.

Giải

Bạn đang xem: Giải bài 9, 10, 11, 12 trang 138 SBT Toán lớp 7 tập 1

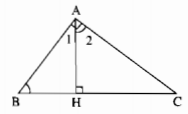
Có thể tìm góc B bằng hai cách:

*Cách 1

Ta có (widehat {{A_1}} + widehat {{A_2}} = widehat {BAC} = 90^circ )                          (1)

Vì ∆AHB vuông tại H nên:

(widehat B + widehat A = 90^circ ) (tính chất tam giác vuông)         (2)

Từ (1) và (2) suy ra: (widehat B = widehat {{A_2}})

*Cách 2

Vì ∆ABC vuông tại A nên: 

(widehat B + widehat C = 90^circ ) (tính chất tam giác vuông)             (1)

Vì ∆AHC vuông tại H nên

(widehat {{A_2}} + widehat C = 90^circ ) (tính chất tam giác vuông)          (2)

Từ (1) và (2) suy ra: (widehat B = widehat {{A_2}}).

Câu 10 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho hình dưới:

a) Có bao nhiêu tam giác vuông trong hình?

b) Tính số đo các góc nhọn ở các đỉnh C, D, E.

Giải

a) Có năm tam giác vuông trong hình:

               ∆ABC vuông tại B

               ∆CBD vuông tại B

               ∆EDA vuông tại D

               ∆DCAvuông tại C

               ∆DCEvuông tại C

b) ∆ABC vuông tại B, suy ra:

(widehat A + widehat {ACB} = 90^circ ) (tính chất tam giác vuông)

(eqalign{
& Rightarrow widehat {ACB} = 90^circ – widehat A = 90^circ – 40^circ = 50^circ cr
& widehat {ACB} + widehat {BC{rm{D}}} = widehat {AC{rm{D}}} = 90^circ cr
& Rightarrow widehat {BC{rm{D}}} = 90^circ – widehat {ACB} = 90^circ – 50^circ = 40^circ cr} )

∆ACD vuông tại C, suy ra:

(widehat A + widehat {C{rm{D}}A} = 90^circ ) (tính chất tam giác vuông)

(eqalign{
& Rightarrow widehat {C{rm{D}}A} = 90^circ – widehat A = 90^circ – 40^circ = 50^circ cr
& widehat {C{rm{D}}A} + widehat {C{rm{D}}E} = widehat {A{rm{D}}E} = 90^circ cr
& Rightarrow widehat {C{rm{D}}E} = 90^circ – widehat {C{rm{D}}A} = 90^circ – 50^circ = 40^circ cr} )

∆DEA vuông tại D, suy ra:

(widehat A + widehat E = 90^circ ) (tính chất tam giác vuông)

( Rightarrow widehat E = 90^circ  – widehat A = 90^circ  – 40^circ  = 50^circ )

Câu 11 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC có (widehat B = 70^circ ,widehat C = 30^circ ). Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H ∈ BC).

a) Tính (widehat {BAC}) 

b) Tính (widehat {A{rm{D}}H})

c) Tính (widehat {HA{rm{D}}})

Giải

a) Trong ∆ABC, ta có:

(widehat {BAC} + widehat B + widehat C = 180^circ ) (tổng ba góc trong tam giác)

Mà (widehat B = 70^circ ;widehat C = 30^circ left( {gt} right))

Suy ra: (widehat {BAC} + 70^circ  + 30^circ  = 180^circ )

Vậy (widehat {BAC} = 180^circ  – 70^circ  – 30^circ  = 80^circ )

b) Ta có: (widehat {{A_1}} = {1 over 2}widehat {BAC} = {1 over 2}.80^circ  = 40^circ ) (Vì AD là tia phân giác của (widehat {BAC}))

Trong ∆ADC ta có (widehat {A{rm{D}}H}) là góc ngoài tại đỉnh D.

Do đó: (widehat {A{rm{D}}H} = widehat {{A_1}} + widehat C) (tính chất góc ngoài của tam giác)

Vậy (widehat {A{rm{D}}H} = 40^circ  + 30^circ  = 70^circ )

c) ∆ADH vuông tại H nên:

(widehat {HA{rm{D}}} + widehat {A{rm{D}}H} = 90^circ ) (tính chất tam giác vuông)

( Rightarrow widehat {HA{rm{D}}} = 90^circ  – widehat {A{rm{D}}H} = 90^circ  – 70^circ  = 20^circ )

Câu 12 trang 138 Sách Bài Tập (SBT) Toán lớp 7 tập 1

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính (widehat {BIC}) biết rằng:

a) ({rm{}}widehat B = 80^circ ,widehat C = 40^circ )

b) (widehat A = 80^circ )

c) (widehat A = m^circ )

Giải

a) Ta có

(widehat {{B_1}} = {1 over 2}widehat {ABC} = {1 over 2}.80^circ  = 40^circ ) (vì BD là tia phân giác của (widehat {ABC}))

(widehat {{C_1}} = {1 over 2}widehat {ACB} = {1 over 2}.40^circ  = 20^circ ) (vì CE là tia phân giác của (widehat {ACB}))

Trong ∆IBC, ta có: (widehat {BIC} + widehat {{B_1}} + widehat {{C_1}} = 180^circ ) (tổng 3 góc trong tam giác)

(widehat {BIC} = 180^circ  – left( {widehat {widehat {{B_1}} + {C_1}}} right) = 180^circ  – left( {40^circ  + 20^circ } right) = 120^circ )

b) Ta có:

(widehat {{B_1}} = {1 over 2}widehat B) (vì BD là tia phân giác (widehat B))

(widehat {{C_1}} = {1 over 2}widehat C) (vì CE là tia phân giác (widehat C))

Trong ∆ABC, ta có:

(widehat A + widehat B + widehat C = 180^circ ) (tổng ba góc trong tam giác)

Suy ra (widehat B + widehat C = 180^circ  – widehat A = 180^circ  – 80^circ  = 100^circ )

Trong ∆IBC, ta có: (widehat {BIC} + widehat {{B_1}} + widehat {{C_1}} = 180^circ )

Vậy (widehat {BIC} = 180^circ  – left( {widehat {{B_1}} + widehat {{C_1}}} right) = 180^circ  – {{widehat B + widehat C} over 2} = 180^circ  – {{100^circ } over 2} = 130^circ )

c) Ta có: (widehat B + widehat C = 180 – m^circ )

Vậy (widehat {BIC} = 180^circ  – {{180^circ  – m^circ } over 2} = 180^circ  – 90^circ  + {{m^circ } over 2} = 90^circ  + {{m^circ } over 2})

Trường

Giải bài tập